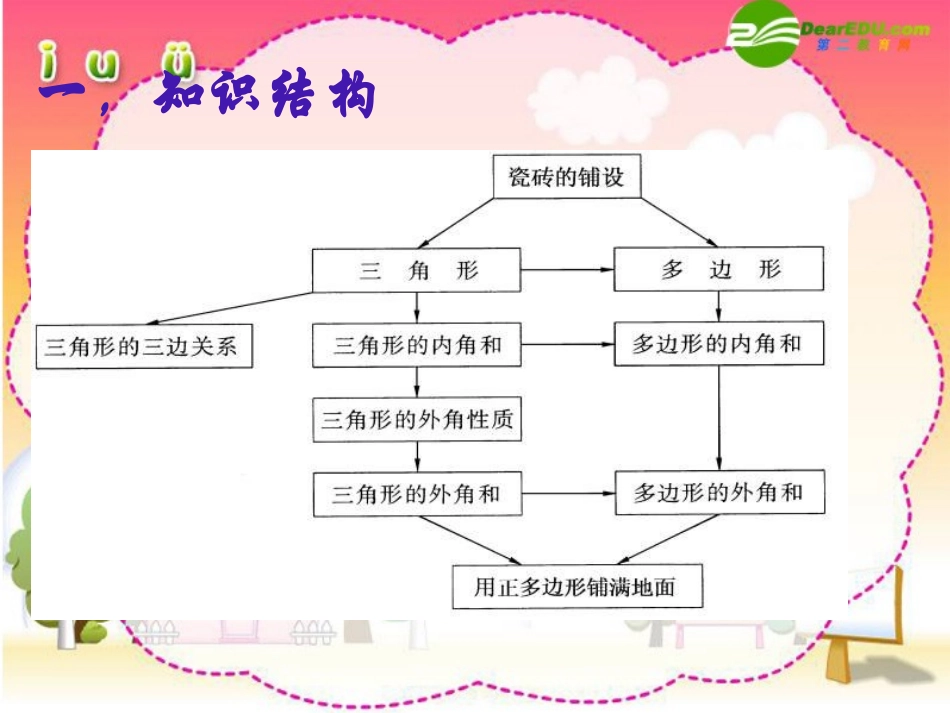
三角形的三边关系的复习三角形的三边关系的复习童联乐童联乐一,知识结构二,热身练习1,等腰三角形的两条边长分别为3厘米和5厘米,则等腰三角形的周长为______厘米;2,等腰三角形的两条边长分别为2厘米和5厘米,则等腰三角形的周长为______厘米;3,判断下列三条线段能否组成三角形A15cm10cm7cmB3cm8cm5cmCa+1a+2a+3(a>0)D三边之比为7︰8︰154,已知三角形的两边长为3和7,则第三条边x的取值范围是______;5,△ABC的三条边长都是整数,且AC=10cm,AB=7cm那么BC的最大长度是___,BC的最小长度是___11或1312三角形任何两边的和大于第三边只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.两边之差第三边两边之和能否能否4<x<10164由由7cm7cm,,5cm5cm,,4cm4cm三条线段能否组成三角形?三条线段能否组成三角形?((11)先画线段)先画线段AB=7cmAB=7cm;;((22)以点)以点AA为圆心,为圆心,5cm5cm长为半径画圆弧:长为半径画圆弧:AB((33)以点)以点BB为圆心,为圆心,4cm4cm长为半径画圆弧,长为半径画圆弧,两弧相交于点两弧相交于点CC;;((44)连接)连接ACAC、、BCBC。。ABCABC就是所要画的三角形。就是所要画的三角形。C三,动手画一画画出这个三角形画出这个三角形3.三角形具有稳定性,并在生活中有广泛的应用。1、三角形的三边关系定理:任何两边的和大于第三边。(1)判断三条已知线段能否组成三角形.(2)已知三角形的两边,求第三边的取值范围:两边之差第三边两边之和(a-b<c<a+b)2.画给定边长的三角形知识梳理:稳定性在生活中的运用举例稳定性在生活中的运用举例::稳定性在生活中的运用举例稳定性在生活中的运用举例::四,例题分析例1,一个三角形的两边长分别为2cm和9cm.(1)若第三边长为奇数,则第三边长为多少?(2)若周长为奇数,则第三边长为多少?解:设第三边为a,则7<a<11∵a为奇数∴a=9例2在等腰三角形ABC中,AB=AC,周长为16cm,AC边上的中线BD把△ABC分成周长差为4cm的两个三角形,求△ABC各边的长.ABCD五,实践和应用湖边有A,B两个村庄(如图),从A到B有两条路可走,即APB,和AMNB,后一条路必定比前一条路短,你能运用三角形三边关系说明理由吗?APBMN