动力学课后思考题答案VIP免费

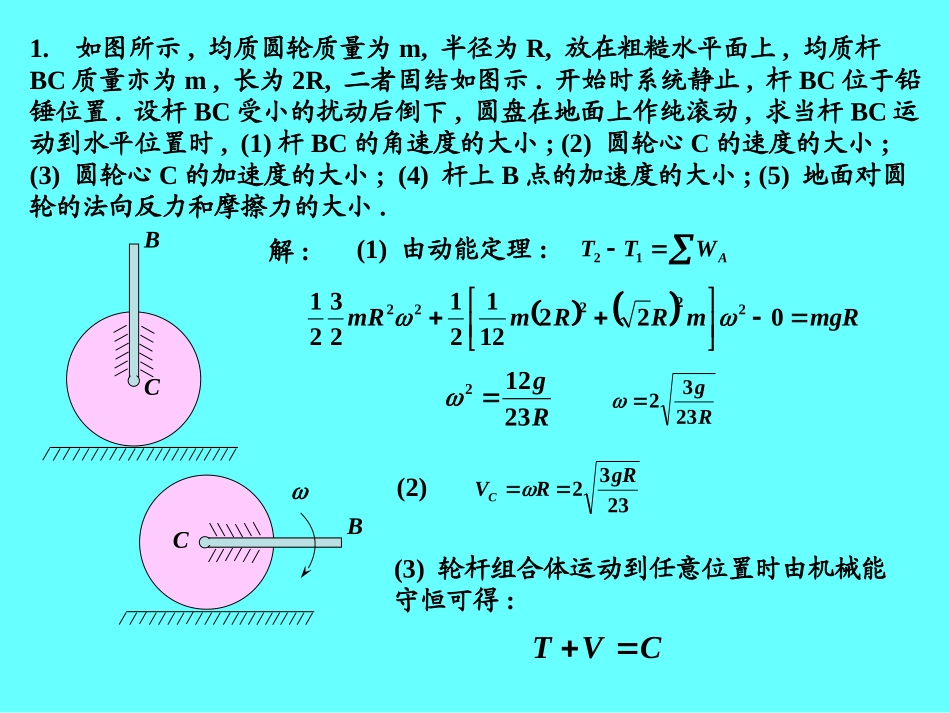
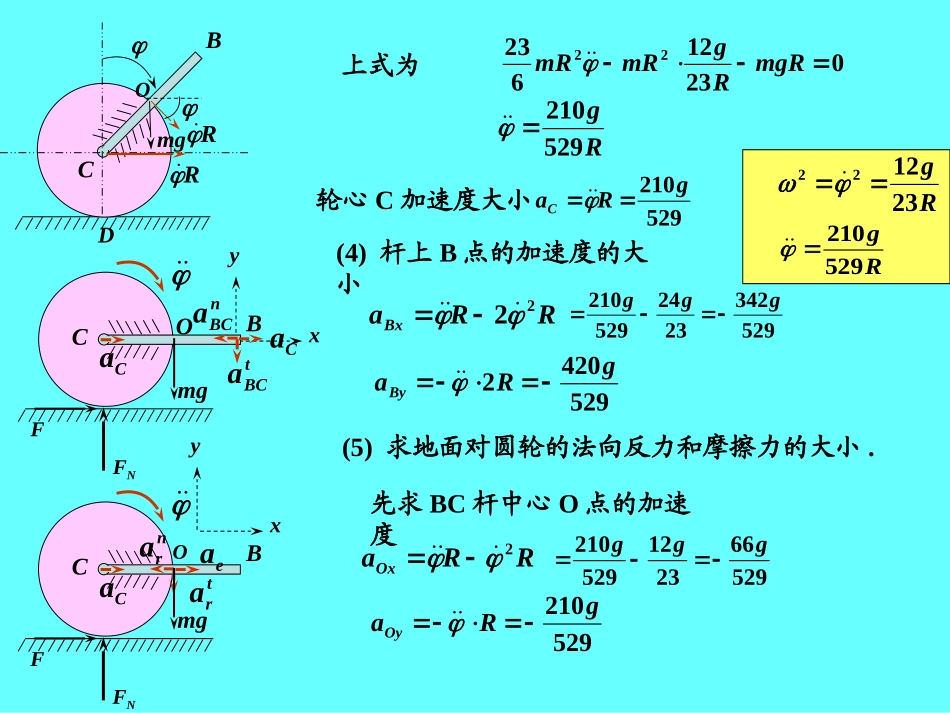
1.如图所示,均质圆轮质量为m,半径为R,放在粗糙水平面上,均质杆BC质量亦为m,长为2R,二者固结如图示.开始时系统静止,杆BC位于铅锤位置.设杆BC受小的扰动后倒下,圆盘在地面上作纯滚动,求当杆BC运动到水平位置时,(1)杆BC的角速度的大小;(2)圆轮心C的速度的大小;(3)圆轮心C的加速度的大小;(4)杆上B点的加速度的大小;(5)地面对圆轮的法向反力和摩擦力的大小.CBCB解:(1)由动能定理:AWTT12mgRmRRmmR02212121232122222Rg23122Rg2332(2)2332gRRVC(3)轮杆组合体运动到任意位置时由机械能守恒可得:CVTCcosmgRRmsinRcosRRmmR22222222212121212321选过C水平面为重力势能零点,对任意位置,系统有CcosmgRJmVJOOD222212121CBmgRRODCcosmgRmRcosmRmRmR222222226143CcosmgRcosmRmR22221223两边对时间t求导数026233222sinmgRsinmRcosmRmR026232222sinmgRsinmRcosmRmR当=900时Rg231222上式为0231262322mgRRgmRmRxyOCBCaCanBCatBCaNFFmgCBmgRROD上式为0231262322mgRRgmRmRRg529210轮心C加速度大小529210gRaC(4)杆上B点的加速度的大小RRaBx22Rg231222Rg5292105293422324529210ggg5294202gRaByCBCaeanratraNFFmgO(5)求地面对圆轮的法向反力和摩擦力的大小.xy先求BC杆中心O点的加速度RRaOx2529662312529210ggg529210gRaOy轮心C加速度大小529210gRaC(5)求地面对圆轮的法向反力和摩擦力的大小.RRaOx2529210gRaOyxy由动量定理:eiiiFamx方向:y方向:FmamaOxCmgmgmgF5291445296652921052966gmgFmaNOy2mgmaFOyN2mgmgmgFN5298485292102CBCaeanratraNFFmgOmg另解:求解某时刻的加速度和约束力,还可用达朗伯原理.CarOyarOxaeOaCBOgOMgCMmgmgrgOxFrgOyFegOFgCFRmFgCRmFegORmFrgOyRmFrgOx2221mRMgC231mRMgONFFDRg2312220Dm0mgRRFRFRFRFMMrgOxrgOyegOgCgOgC031212222222mgRRmRmRmRmmRmRmgRRmRmRm2222365Rg5292100X0YmgF529144mgFN529848BCBCOgm2解:系统有两个自由度,选x、为广义坐标2.如图所示,均质圆轮质量为m1,半径为R,放在粗糙水平面上,均质杆BC质量为m2,长为2R,用铰链连接于轮心C.开始时系统静止,杆BC位于铅锤位置.杆BC受小的扰动后倒下,设圆盘在地面上作纯滚动,求当杆BC运动到水平位置时,(1)杆BC的角速度的大小;(2)圆轮心C的速度的大小;(3)杆BC的角加速度的大小;(4)圆轮心C的加速度的大小;(5)地面对圆轮的法向反力和摩擦力的大小.xxRFNFFNFxCCxFCyF由动量定理的水平方向投影取系统分析:tFdtcosRxmxm0210取圆轮分析:由对质心的动量矩定理dtFRORxRmt02121tFdtcosRxmxm0210dtFRORxRmt02121BCOgm2xRtFdtcosRmxmxm0221dtFxmt0121两式联立可得:023221cosRmxmxm(1)210322143222222221cosgRmcosRxmRmxmxm由系统的动能定理:AWTT12BCx当=900由(1)式:0x即VC=0.(2)式可化作:gRmRm222232Rg23Rg232即是即BCBCOxgm2R1023221cosRmxmxm2cos1cos322143222222221gRmRxmRmxmxm0xRg23xBCx将(1)式两边对t求导30sincos23222121...