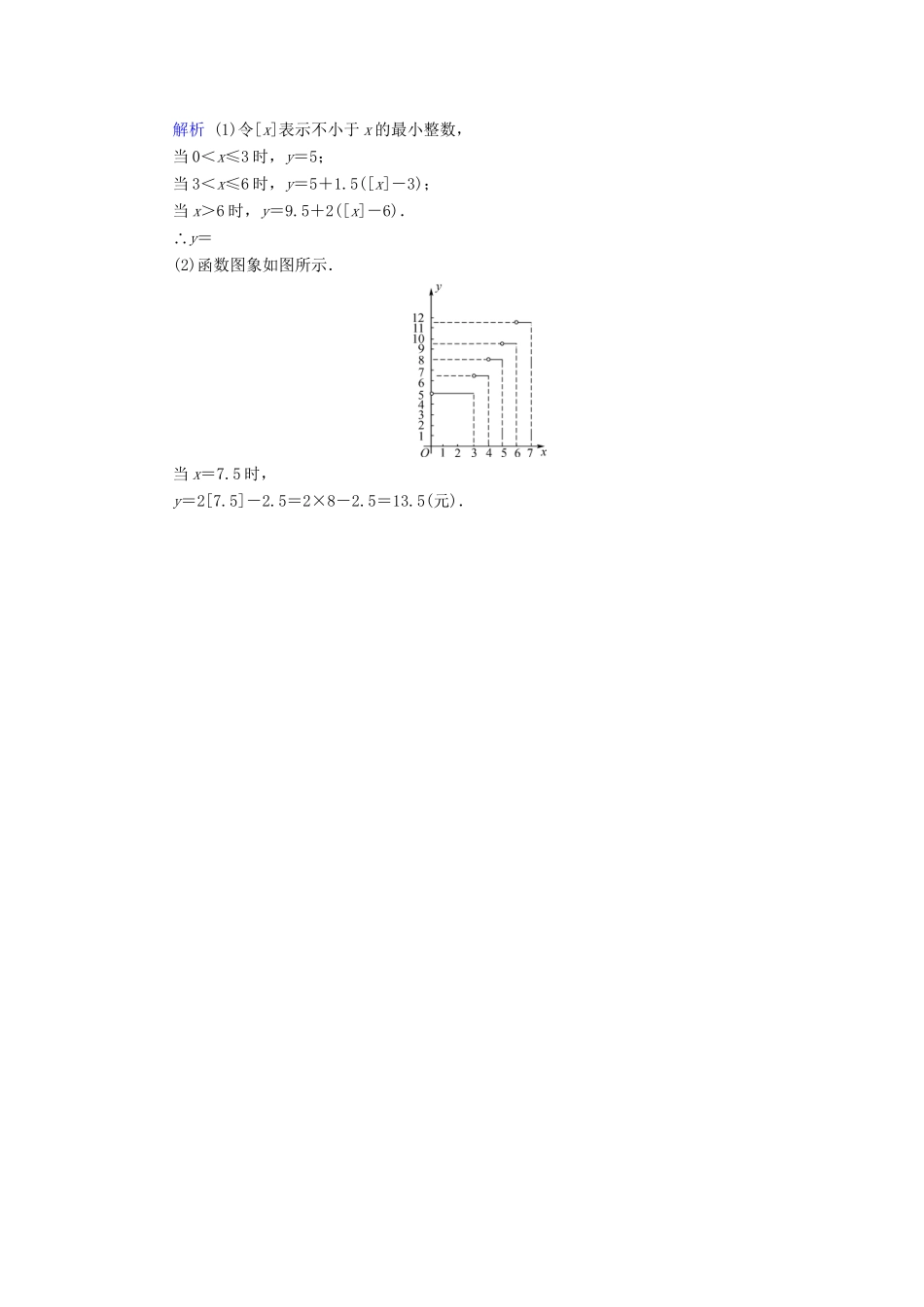
【创优导学案】届高考数学总复习第二章函数与导数2-1课后巩固提升(含解析)新人教A版(对应学生用书P373解析为教师用书独有)(时间:45分钟满分:100分)一、选择题(本大题共6小题,每小题6分,共36分)1.函数f(x)=log2(3x+1)的值域为()A.(0∞,+)B.[0∞,+)C.(1∞,+)D.[1∞,+)解析A∵3x+1>1,∴f(x)=log2(3x+1)>log21=0.2.已知集合A={x|0≤x≤4},集合B={y|0≤y≤2},按照下列关系能构成集合A到集合B的映射的是()A.f:x→y=x,x∈AB.f:x→y=x,x∈AC.f:x→y=x,x∈AD.f:x→y=x,x∈A解析B对于A、C、D,集合A中的元素4在集合B中没有元素与之对应,故不能构成映射.3.下列各组函数f(x)与g(x)的图象相同的是()A.f(x)=x,g(x)=()2B.f(x)=x2,g(x)=(x+1)2C.f(x)=x,g(x)=elnxD.f(x)=|x|,g(x)=解析D选项A、C中函数的定义域不同,B中函数的对应关系不同,故选D.4.若f(x)=则f(-3)的值为()A.2B.8C.D.解析Cf(-3)=f(-1)=f(1)=f(3)=2-3=.5.设函数f(x)=则满足f(x)≤2的x的取值范围是()A.[-1,2]B.[0,2]C.[1∞,+)D.[0∞,+)解析D当x≤1时,21-x≤2,解得x≥0,所以0≤x≤1;当x>1时,1-log2x≤2,解得x≥,所以x>1.综上可知x≥0.6“.若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为同族函”数,则函数解析式为y=x2+1,值域为{1,3}的同族函数有()A.1个B.2个C.3个D.4个解析C由x2+1=1得x=0,由x2+1=3得x=±,∴函数的定义域可以是{0,},{0,-},{0,,-},共3个.二、填空题(本大题共3小题,每小题8分,共24分)7.(·江苏高考)函数f(x)=的定义域为________.解析要使函数f(x)=有意义,则需解得01),则x=,∴f(t)=lg,f(x)=lg(x>1),f(21)=-1.【答案】-1三、解答题(本大题共3小题,共40分)10.(12分)求下列函数的定义域:(1)f(x)=;(2)y=lg(x-1)+lg+.解析(1)⇒x<4且x≠3,故该函数的定义域为(∞-,3)∪(3,4).(2)即或x<-1,解得10时,f(g(x))=f(x-1)=(x-1)2-1=x2-2x;当x<0时,f(g(x))=f(2-x)=(2-x)2-1=x2-4x+3.即f(g(x))=同理g(f(x))=12.(16分)某市出租车起步价为5元,起步价内最大行驶里程为3km,以后3km内每1km加收1.5元,再超过3km后,每1km加收2元.(不足1km按1km计算)(1)写出出租费用y关于行驶里程x的函数关系式;(2)作出函数图象,并求行驶7.5km时的出租费用.解析(1)令[x]表示不小于x的最小整数,当0<x≤3时,y=5;当3<x≤6时,y=5+1.5([x]-3);当x>6时,y=9.5+2([x]-6).∴y=(2)函数图象如图所示.当x=7.5时,y=2[7.5]-2.5=2×8-2.5=13.5(元).