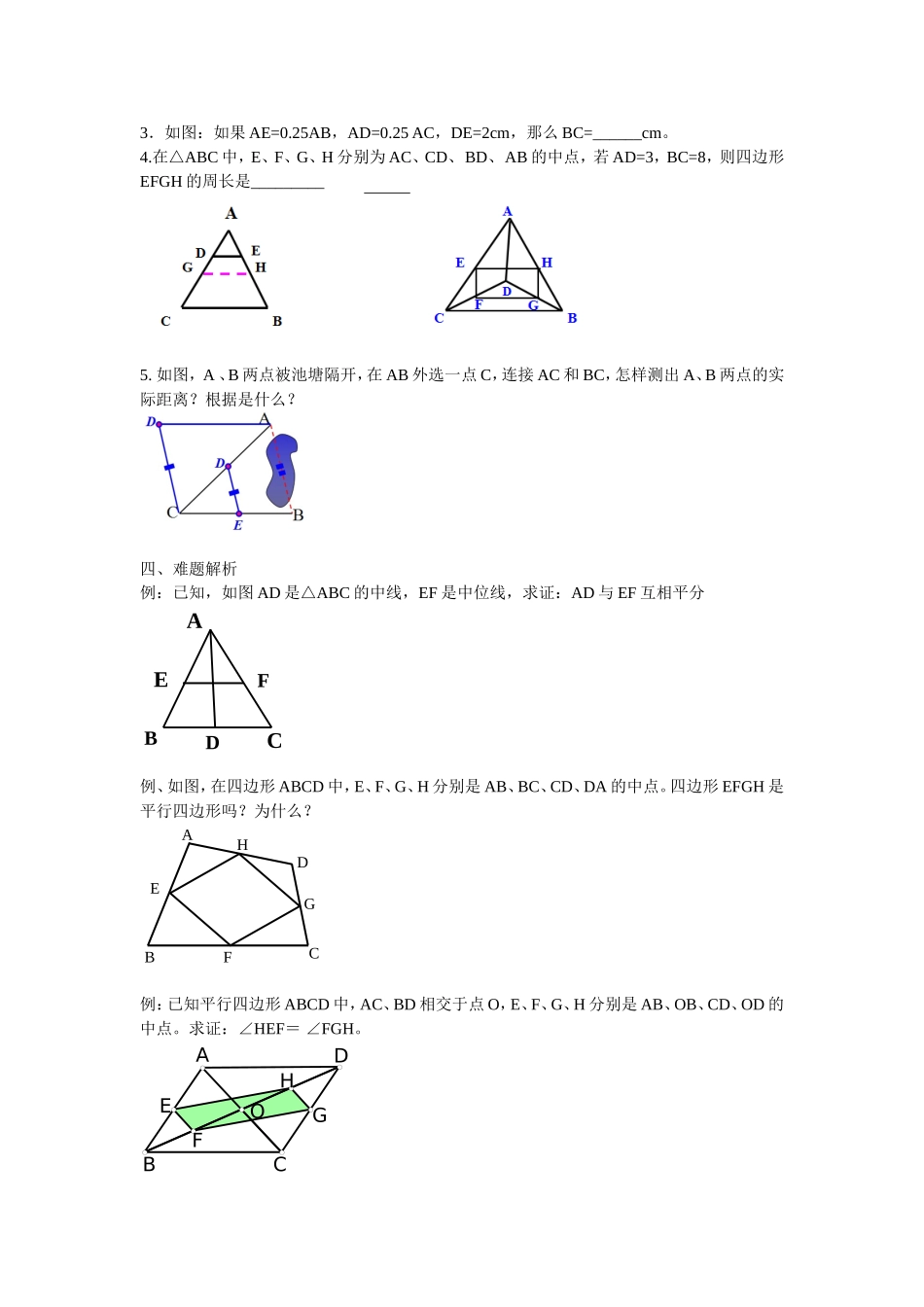
18.1.2平行四边形的判定4教学目标:1.理解三角形中位线的概念,掌握它的性质.2.能较熟练地应用三角形中位线性质进行有关的证明和计算.3.能运用综合法证明有关三角形中位线性质的结论.理解在证明过程中所运用的归纳、类比、转化等思想方法.教学重点:掌握和运用三角形中位线的性质.教学难点:三角形中位线性质的证明(辅助线的添加方法).教学过程:一、创设情境现有一张三角形纸片,你能通过裁剪,将它拼成一个平行四边形吗?引出中位线定义:连结三角形两边中点的线段叫三角形的中位线。思考:三角形的中位线与三角形的中线有什么区别?中位线是两个中点的连线,而中线是一个顶点和对边中点的连线。二、性质探究思考:1、三角形的中线有哪些性质?2、三角形的中位线有哪些性质?在△ABC中,DE是△ABC的中位线,DE与BC有何位置与数量关系?并证明三角形中位线的性质:三角形的中位线平行于第三边,并且等于第三边的一半(中位线定理可证线段的倍分关系.)练习:(1)△DEF的周长与△ABC的周长有什么关系?(2)△DEF的面积与△ABC的面积有什么关系?三、应用口答:(1)三角形的周长为18cm,这个三角形的三条中位线围成三角形的周长是多少?为什么?(2)如图,E是平行四边形ABCD的AB边上的中点,且AD=10cm,那么OE=_______cm。ABDCEO1.△ABC中,D、E分别是AB、AC的中点,BC=10cm,则DE=______.2.△ABC中,D、E分别是AB、AC的中点,∠A=50°,∠B=70°,则∠AED=________EDCBA3.如图:如果AE=0.25AB,AD=0.25AC,DE=2cm,那么BC=______cm。4.在△ABC中,E、F、G、H分别为AC、CD、BD、AB的中点,若AD=3,BC=8,则四边形EFGH的周长是_________5.如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?四、难题解析例:已知,如图AD是△ABC的中线,EF是中位线,求证:AD与EF互相平分ABCDEF例、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是平行四边形吗?为什么?ABCDEFGH例:已知平行四边形ABCD中,AC、BD相交于点O,E、F、G、H分别是AB、OB、CD、OD的中点。求证:∠HEF=∠FGH。GHFOEDCBA例:已知:E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连结AE,分别交BC、BD于点F、G,连接AC交BD于O,连结OF.求证:AB=2OF挑战自我:如图,△ABC是锐角三角形。分别以AB,AC为边向外侧作等边三角形ABM和等边三角形CAN。D,E,F分别是MB,BC,CN的中点,连结DE,EF。求证:DE=EF四、小结及反思