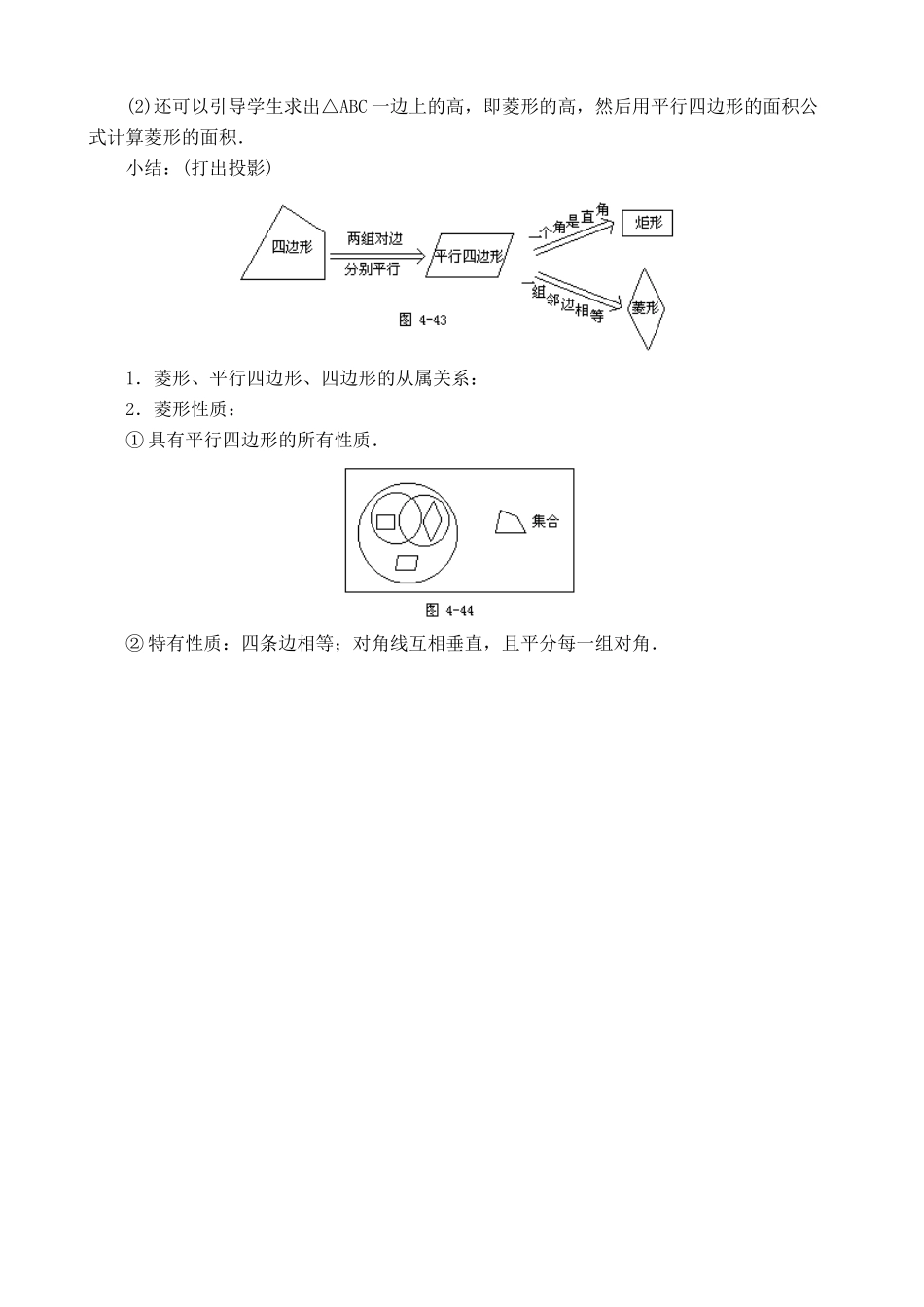
特殊的平行四边形一、教学目标1.掌握菱形的定义,知道菱形与平行四边形的关系.2.掌握菱形的性质定理1和性质定理2,井能用定义判定一个四边形是菱形.4.使学生能够灵活运用菱形知识解决有关问题,提高能力.5.通过教具的演示培养学生的观察能力并提高学生的学习兴趣.6.根据平行四边形与矩形、菱形的从属关系,通过画图向学生渗透集合思想.二、教学重点、难点1.重点:菱形的性质定理.2.难点:把菱形的性质和直角三角形的知识综合应用.三、教学方法观察分析讨论相结合的方法.四、教学手段(做一个短边可以运动的平行四边形)投影仪、透影胶片.五、教学过程(一)复习提问(用投影仪打出)1.什么叫做平行四边形?什么叫矩形?平行四边形和矩形之间的关系是什么?2.矩形中对角线与大边的夹角为36°,求小边所对的两条对角线的夹角.3.矩形的一个角的平分线把较长的边分成5cm、3cm,求矩形的周长。(二)引入新课我们已经学习了一种特殊的平行四边形——矩形,其实还有另外的特殊平行四边形,这时可将事先按课本中图4-33做成的一个短边也可以活动的教具进行演示,如图4-39,改变平行四边形的边,使之一组邻边相等,引出菱形概念.(三)讲解新课1.菱形定义:有一组邻边相等的平行四边形叫做菱形.讲解这个定义时,要抓住概念的本质,应突出两条:(1)强调菱形是平行四边形.(2)一组邻边相等.2.菱形的性质:教师强调,菱形既然是特殊的平行四边形,因此它就具有平行四边形的一切性质,此外由于它比平行四边形多了“一组邻边相等”的条件,和矩形类似,也比平行四边形增加了一些特殊性质.下面研究菱形的性质:师:同学们根据菱形的定义结合图形猜一下菱形有什么性质(让学生们讨论,并引导学生分别从边、角、对角线三个方面分析).生:因为菱形是有一组邻边相等的平行四边形,所以根据平行四边形对边相等的性质可以得到.菱形性质定理1:菱形的四条边都相等.由菱形的四条边都相等,根据平行四边形对角线互相平分,可以得到菱形性质定理2:菱形的对角线互相垂直并且每一条对角线平分一组对角.引导学生完成定理的规范证明.师:观察图4-40,菱形ABCD被对角线分成的四个直角三角形有什么关系?生:全等.师:它们的底和高和两条对角线有什么关系?生:分别是两条对角线的一半.师:如果设菱形的两条对角线分别为a、b,则菱形的面积为什么?教师指出当不易求出对角线长时,就用平行四边形面积的一般计算方法计算菱形面积.例2已知:如图4-41,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F.求证:四边形AEDF是菱形.引导学生用菱形定义来判定.例3已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC,BD相交于点O,如图4-42,求这个菱形的对角线长和面积.(1)按教材的方法求面积.(2)还可以引导学生求出△ABC一边上的高,即菱形的高,然后用平行四边形的面积公式计算菱形的面积.小结:(打出投影)1.菱形、平行四边形、四边形的从属关系:2.菱形性质:①具有平行四边形的所有性质.②特有性质:四条边相等;对角线互相垂直,且平分每一组对角.