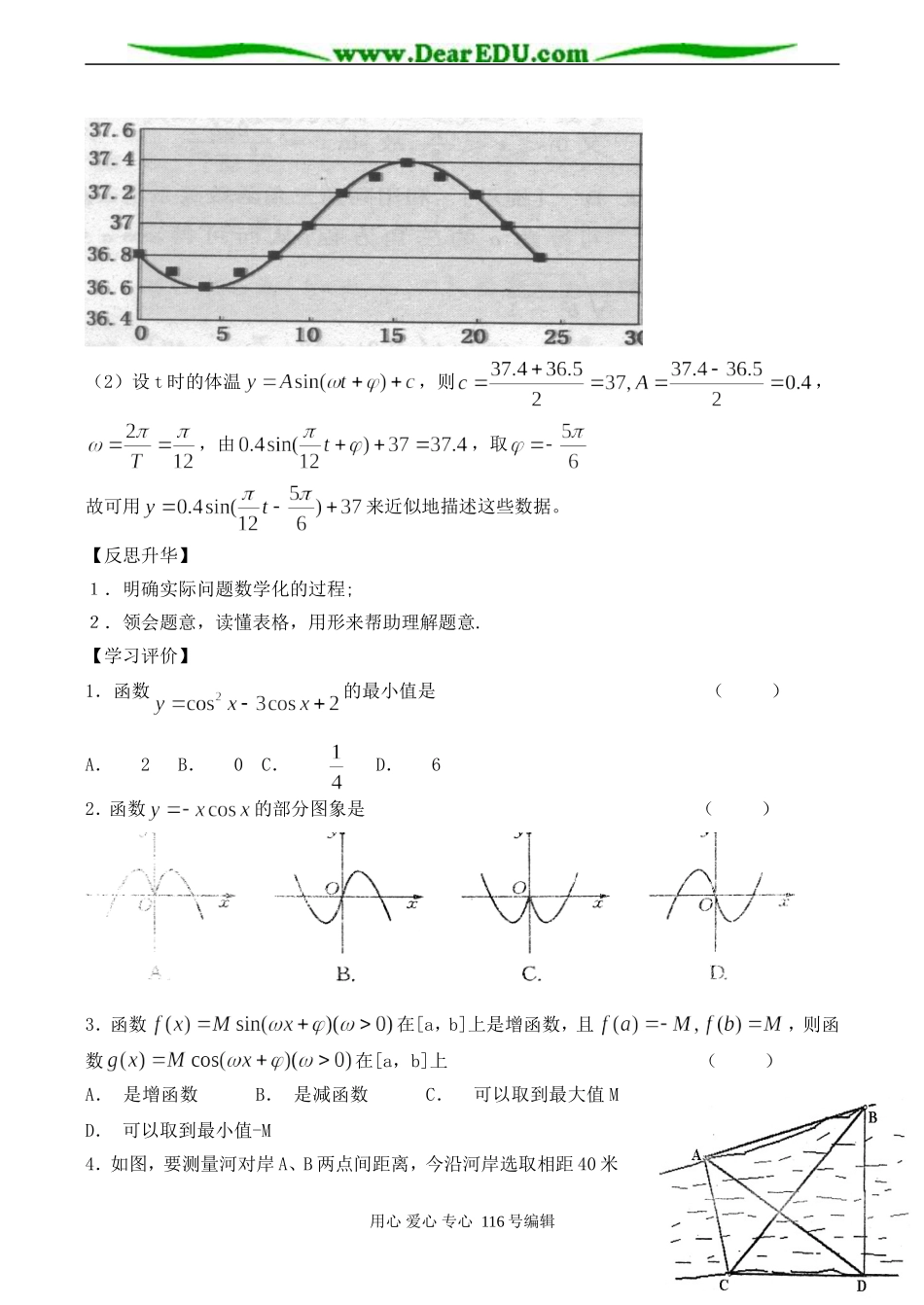
高一数学三角函数的应用(2)【学习目标】1.能应用三角函数的图象与性质解决有关实际问题.2.进一步体会三角函数是描述周期现象的重要数学模型.【题型示例】例1如图,某地一天6时到14时的温度变化曲线近似满足:(1)求这一天从6时到14时的最大温差;(2)写出这段曲线的函数解析式。【分析】仔细观察图象,注意分析图象特征。【解】(1)由图示,这段时间的最大温差是℃(2)图中从6时到14时的图象是函数的半个周期∴,解得由图示,这时,将代入上式,可取综上,所求的解析式为()例2设是某港口水的深度y(米)关于时间t(时)的函数,其中.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:t03691215182124y1215.112.19.111.914.911.98.912.1经长期观察,函数的图象可以近似地看成函数的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是()A.B.C.D.用心爱心专心116号编辑Oxy61014102030(例1)【分析】通过观察,发现表格中数据的关系、作用,找出对应的最大值、最小值,周期等。【解】,所以。故选B例3受日月的引力,海水会发生涨落,这种现象叫做潮汐,在通常情况下,船在涨潮时驶进航道,靠近船坞,卸货后落潮时返回海洋,某港口水的深度y(米)是时间t(240t,单位:时)的函数,记作y=f(t),下面是该港口在某季节每天水深的数据。t(时)0361215182124y(米)10.013.09.910.013.010.17.010.0根据数据发现y=f(t)的曲线可近似的看作函数的图象,请求出函数解析式,(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时,认为是安全的(船舶停靠时,船底只需不碰海底即可),某船吃水深度(船底离水面的距离)为6.5米,如果该船想在同一天内安全进出港,问它至多能在港内停留多少时间?(忽略进出港所需时间)【分析】学会观察,通过对表格中的数据进行处理,得到【解】由数据直振幅A=3,b=10,周期T=12,所以该函数为(2)由,知道,又得到所以或,得或,所以此船可以1时进港,17时离港,因此它最多能在港内停留16个小时。【拓展创新】生物节律是描述体温、血压和其他变化的生理变化的每日生物模型.下表中给出了在24小时期间人的体温的变化(从夜间零点开始计时).时间024681012141618202224温度36.836.736.636.736.83737.237.337.437.337.237.036.8(1)作出这些数据的散点图;(2)选用一个三角函数来近似描述这些数据;(3)和散点图一起,画出(2)中所选函数的图象.【分析】由数据的散点图,进一步寻找两个变量之间的关系,找出相应的函数关系式【解】(1)散点图:用心爱心专心116号编辑(2)设t时的体温,则,,由,取故可用来近似地描述这些数据。【反思升华】1.明确实际问题数学化的过程;2.领会题意,读懂表格,用形来帮助理解题意.【学习评价】1.函数的最小值是()A.2B.0C.D.62.函数的部分图象是()3.函数在[a,b]上是增函数,且,则函数在[a,b]上()A.是增函数B.是减函数C.可以取到最大值MD.可以取到最小值-M4.如图,要测量河对岸A、B两点间距离,今沿河岸选取相距40米用心爱心专心116号编辑10md5m的C、D两点,测得∠ACB=60°,∠BCD=45°,∠ADB=60°,∠ADC=∠ABC=30°,则AB的距离是A.20B.20()C.40D.205.从高出海面hm的小岛A处看正东方向有一只船B,俯角为30°,看正南方向的一只船C的俯角为45°,则此时两船间的距离是()A.B.C.D.6.某人的血压满足关系式,其中f(t)为血压,t为时间,则此人每分钟心跳的次数为()A.60B.70C.80D.907.已知函数f(x)=2sinx(>0)在区间[,]上的最小值是-2,则的最小值等于.8.一个物体相对于某一固定位置的位移y(cm)和时间t(s)之间的一组对应值如下表所示:t00.10.20.30.40.50.60.70.8y-4.0-2.80.02.84.02.80.0-2.8-4.0则可近似地描述该物体的位移y和时间t之间关系的一个三角函数为.9.某星星的亮度变化周期是10天,此星星的平均亮度为3.8星等,最高亮度距离平均亮度0.2星等,则可近似地描述此星星亮度与时间之间关系的一个三角函数为.10.如图,一个半径为10米的水轮按逆时针方向每分钟转4圈,记水轮上的点P到水面的距离为d米(当点P在水面下时...