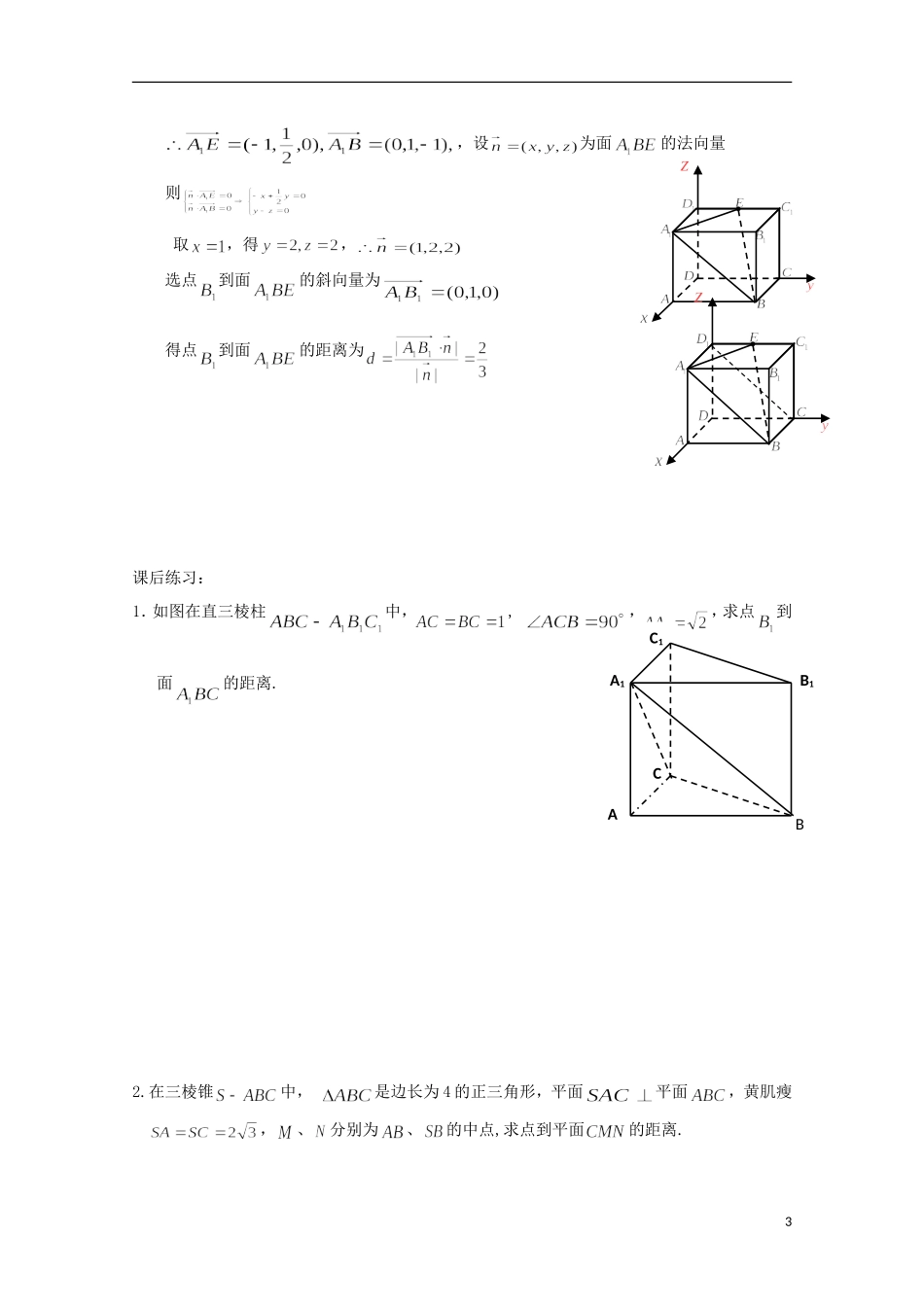
课题:立体几何中的向量方法求空间距离(1)【教学简案】课时:06课型:新授课教学目标:利用向量方法求解空间距离问题,可以回避此类问题中大量的作图、证明等步骤,而转化为向量间的计算问题.(1)点到平面的距离:1.(一般)传统方法:利用定义先作出过这个点到平面的垂线段,再计算这个垂线段的长度;2.还可以用等积法求距离;3.向量法求点到平面的距离.在中,又(其中为斜向量,为法向量)例1:如图,已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.分析:由题设可知CG、CB、CD两两互相垂直,可以由此建立空间直角坐标系.用向量法求解,就是求出过B且垂直于平面EFG的向量,它的长即为点B到平面EFG的距离.解:如图,设4i,4j,2k,以i、j、k为坐标向量建立空间直角坐标系C-xyz.由题设C(0,0,0),A(4,4,0),B(0,4,0),D(4,0,0),E(2,4,0),F(4,2,0),G(0,0,2).∴(2,0,0)BE�,(4,2,0)BF�,(0,4,2)BG�,(2,4,2)GE�,1(2,2,0)EF�.设BM平面EFG,M为垂足,则M、G、E、F四点共面,由共面向量定理知,存在实数a、b、c,使得BMaBEbBFcBG�(1)abc,∴(2,0,0)(4,2,0)(0,4,2)BMabc�=(2a+4b,-2b-4c,2c).由平面EFG,得BMGE,BMEF,于是0BMGE�,0BMEF�.∴(24,24,2)(2,4,2)0(24,24,2)(2,2,0)01abbccabbccabc整理得:,解得1511711311abc.∴BM=(2a+4b,-2b-4c,2c)=.∴222226211||11111111BM�故点B到平面EFG的距离为.说明:用向量法求点到平面的距离,常常不必作出垂线段,只需利用垂足在平面内、共面向量定理、两个向量垂直的充要条件解出垂线段对应的向量就可以了.例2:如图,在正方体中,棱长为1,为的中点,求下列问题:(1)求到面的距离;解:如图,建立空间直角坐标系,则2,设为面的法向量则取,得,选点到面的斜向量为得点到面的距离为课后练习:1.如图在直三棱柱中,,,,求点到面的距离.2.在三棱锥中,是边长为4的正三角形,平面平面,黄肌瘦,、分别为、的中点,求点到平面的距离.3B1A1BC1AC教学反思:4SABCNMO