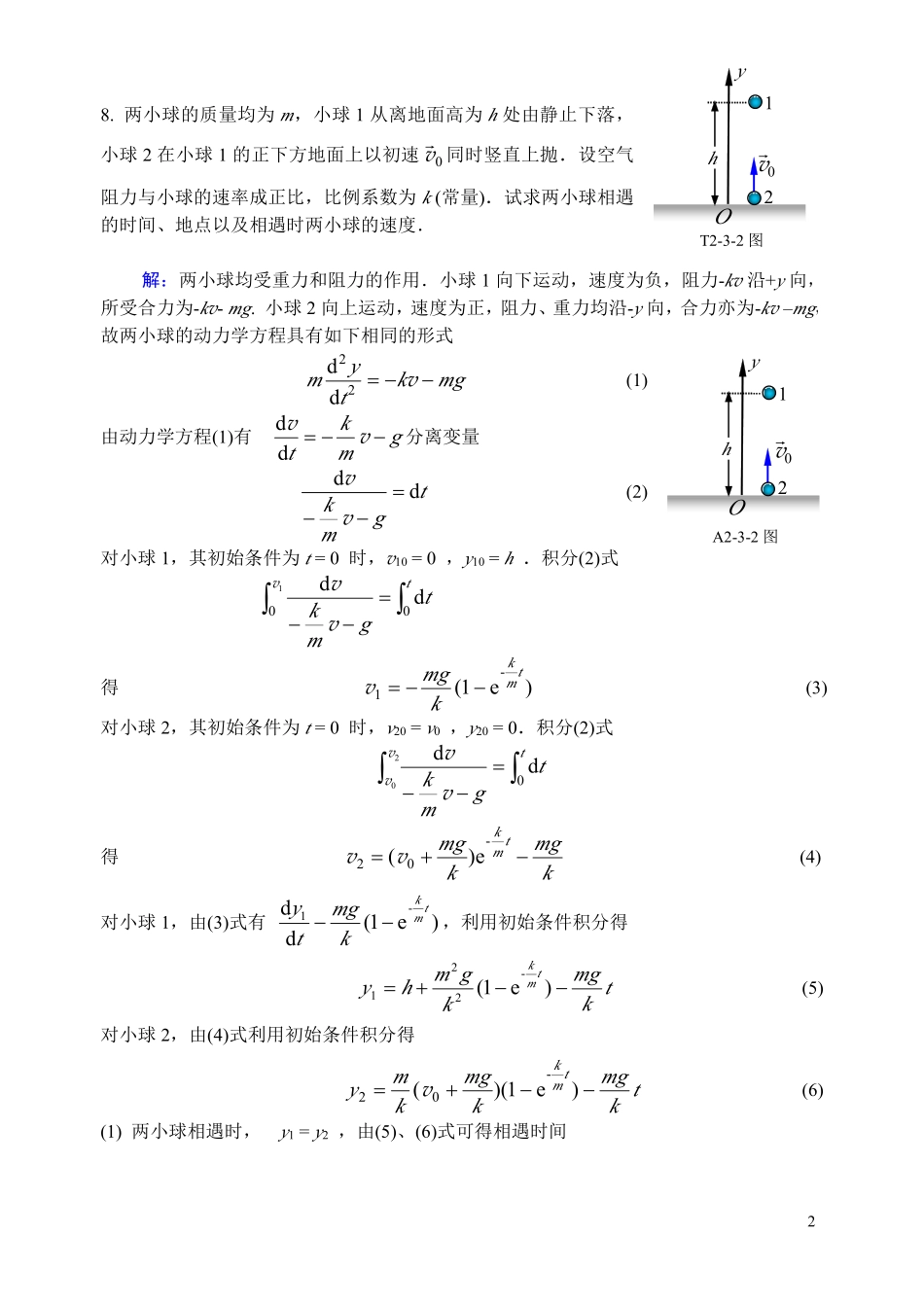
1第2章动力学基本定律补充题1.一质量为m的质点以不变速率v沿T2-2-10图中正三角形ABC的水平光滑轨道运动.质点越过A角时,轨道作用于质点的冲量的大小为vm3.2.一质点受力ixF��23=(SI)作用,沿x轴正方向运动.在从x=0到x=2m的过程中,力F作功为8J.3.一个质点在几个力同时作用下的位移为:kjir����654+−=∆(SI),其中一个恒力为:kjiF����953+−−=(SI).这个力在该位移过程中所作的功为67J.4.一质点在如图所示的坐标平面内作圆周运动,有一力)(0jyixFF���+=作用在质点上.在该质点从坐标原点运动到)2,0(R位置过程中,力F�对它所作的功为=202RF5.质量为m=0.5kg的质点在xOy平面内运动,其运动方程为x=5t,y=0.5t2(SI),从t=2s到t=4s这段时间内,外力对质点作的功为3J.6.一长为l,质量为m的匀质链条,放在光滑的桌面上,若其长度的1/5悬挂于桌边下,将其慢慢拉回桌面,需做功mgl501.7一质量为m的质点在指向圆心的平方反比力2/rkF−=的作用下,作半径为r的圆周运动,此质点的速度=vmrk.若取距圆心无穷远处为势能零点,它的机械能=Erk2−.T2-2-10图ABCXYROT2-2-14图28.两小球的质量均为m,小球1从离地面高为h处由静止下落,小球2在小球1的正下方地面上以初速0v�同时竖直上抛.设空气阻力与小球的速率成正比,比例系数为k(常量).试求两小球相遇的时间、地点以及相遇时两小球的速度.解:两小球均受重力和阻力的作用.小球1向下运动,速度为负,阻力-kv沿+y向,所受合力为-kv-mg.小球2向上运动,速度为正,阻力、重力均沿-y向,合力亦为-kv–mg,故两小球的动力学方程具有如下相同的形式mgktym−−=v22dd(1)由动力学方程(1)有gmkt−−=vvdd分离变量tgmkdd=−−vv(2)对小球1,其初始条件为t=0时,v10=0,y10=h.积分(2)式∫∫=−−ttgmk00dd1vvv得)e1(-1tmkkmg−−=v(3)对小球2,其初始条件为t=0时,v20=v0,y20=0.积分(2)式∫∫=−−ttgmk0dd20vvvv得kmgkmgtmk−+=-02e)(vv(4)对小球1,由(3)式有)e1(dd-1tmkkmgty−−,利用初始条件积分得tkmgkgmhytmk−−+=)e1(-221(5)对小球2,由(4)式利用初始条件积分得tkmgkmgkmytmk−−+=)e1)((-02v(6)(1)两小球相遇时,y1=y2,由(5)、(6)式可得相遇时间T2-3-2图10v�yh2OA2-3-2图10v�yh2O3)1ln(0vmkhkmt−−=∗(7)(2)将(7)代入(5)或(6)式得相遇地点为)1ln()1(0220vvmkhkgmhkmgy−++=∗(8)(3)将(7)式分别代入(3)和(4)中可得相遇速度:001)]1(1[vvvghmkhkmg−=−−−=∗(9)mkhghkmgmkhkmg−−=−−+=∗)()1)((00002vvvvv(10)9.已知一水桶以匀角速度ω绕自身轴z转动,水相对圆筒静止,求水面的形状(z-r关系).解:以水表面任一小体积隔离体m作为研究对象,m受力为重力mg及水对水面m的作用力N(⊥水面),稳定时无切向力(见A2-3-6图)m作匀速圆周运动ra��2ω−=Z方向0cos=−mgNθ(1)-r方向rmN2sinωθ=(2)由(1)、(2)式有rzgrddtan2==ωθ积分有rrgzzzrd)(d002∫∫=ω得022)2(zrgz+=ω水面是旋转抛物面10.如T2-3-9图所示,砂子从h=0.8m高处下落到以3m⋅s-1的速率水平向右运动的传送带上.取重力加速度g=10m⋅s-2,求传送带给予沙子的作用力.T2-3-7图hT2-3-9图水rOθmmgNθ0zzr•z面A2-3-7图4解:设单位时间内落到传送带上砂子的质量为p.以tttd~+时间内落下的砂子dm为研究对象,视为质点tpmdd=根据质点的动量定理,在dm落到传送带上到与传送带一起运动的过程中0ddddvv����⋅−⋅==mmtFI式中()101sm48.01022,sm3−−⋅=××==⋅=ghvv()0vv���−=pF由A2-3-9矢量图可见,F�与水平方向夹角为�5334tgtg01===−vvα11.矿砂从传送带A落到另一传送带B(如T2-3-10图),其速度的大小11sm4−⋅=v,速度方向与竖直方向成30°角;而传送带B与水平线成15°角,其速度的大小12sm2−⋅=v.如果传送带的运送量恒定,设为1hkg2000−⋅=mq,求矿砂作用在传送带B上的力的大小和方向.解:设在极短时间△t内落在传送带B上矿砂的质量为m,即tqmm∆=,如A2-3-10矢量图所示,矿砂动量的增量()12vvv���mmm−=∆设传送带对矿砂平均作用力为F�,由动量定理,=∆⋅tF�()12vvv���mmm−=∆()����75cos221222112vvvvvv−+=∆−=mqtmF()N21.275cos2422...