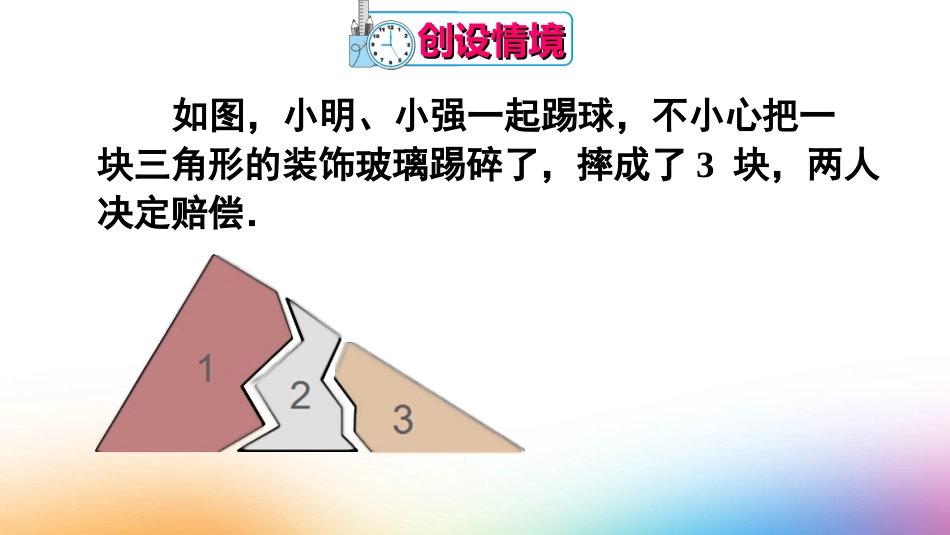
1.什么叫做全等三角形?2.判定两个三角形全等方法有哪些?课前热身课前热身如图,小明、小强一起踢球,不小心把一块三角形的装饰玻璃踢碎了,摔成了3块,两人决定赔偿.321创设情境创设情境你能告诉他们只带其中哪一块去玻璃店,就可以买到一块完全一样的玻璃吗?321创设情境创设情境12.212.2三角形全等的判定三角形全等的判定第3课时角边角和角角边•学习目标:1.经历探索三角形全等条件的过程,掌握判定三角形全等的基本事实“ASA”和定理“AAS”2.运用•学习重、难点:重点:用“ASA”、“AAS”来判定两个三角形全等;用全等证明边相等、角相等难点:如何引导发现“ASA”、“AAS”来确定两个三角形全等;规范书写格式推进新课推进新课问题1先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B(即两角和它们的夹边分别相等).把画好的△A′B′C′剪下来,放到△ABC上,它们全等吗?探究“探究“ASA”ASA”判定方法判定方法知识点1探究DEA′B′C′画法:(1)画A′B′=AB=10;(2)在A′B′的同旁画∠A′=∠A=60°,∠B′=∠B=45°,两边相交于点C′.△ABCAB∠A∠B1060°45°推进新课推进新课探究“探究“ASA”ASA”判定方法判定方法知识点1△ABCAB∠A∠B①20cm70°55°②18cm70°65°③·········基本事实:两角和它们的夹边分别相等的两个三角形全等(简称为“角边角”或“ASA”).也就是说,三角形的两个角的大小和它们的夹边的长度确定了,这个三角形的形状、大小就确定了。几何语言:在△ABC和△A′B′C′中,∴△ABC≌△A′B′C′(ASA).基本事实:两角和它们的夹边分别相等的两个三角形全等(简称为“角边角”或“ASA”).∠A=A′∠,AB=A′B′,∠B=∠B′,B`A`C′已知:如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.推论推论------判定方法“判定方法“AAS”AAS”知识点2推进新课推进新课也就是说,三角形的两个角的大小和其中一个角的对边的长度确定了,这个三角形的形状、大小就确定了。归纳概括“AAS”判定方法:两角和其中一个角的对边分别相等的两个三角形全等(简称为“角角边”或“AAS”).几何语言:在△ABC和△A′B′C′中,∴△ABC≌△A′B′C′(AAS).∠A=A′∠,∠B=∠B′,AC=A′C′,B`A`C′归纳概括“AAS”判定方法:两角和其中一个角的对边分别相等的两个三角形全等(简称为“角角边”或“AAS”).如图,小明、小强一起踢球,不小心把一块三角形的装饰玻璃踢碎了,摔成了3块,两人决定赔偿.你能告诉他们只带其中哪一块去玻璃店,就可以买到一块完全一样的玻璃吗?321创设情境创设情境创设情境创设情境1、判断.(1)有两条边和一个角对应相等的两个三角形全等.()(2)有两个角和一条边对应相等的两个三角形全等.()(3)三角分别相等的两个三角形全等()×√随堂演练随堂演练×2.已知:如图,∠ABC=∠DEF,AB=DE,要证明△ABC≌△DEF,(1)若以“SAS”为依据,还须添加的一个条件为____________.(2)若以“ASA”为依据,还须添加的一个条件为_____________.(3)若以“AAS”为依据,还须添加的一个条件为_____________.随堂演练随堂演练ABCFED3、如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:AD=AE.随堂演练随堂演练CDABE4、(选做)如图,E,F在线段AC上,AD∥CB,AE=CF.若∠B=∠D,求证:DF=BE.ABCDEF随堂演练随堂演练变式:若将条件“∠B=D”∠变为“DFBE”∥,那么原结论还成立吗?若成立,请证明;若不成立,请说明理由.ABCDEF随堂演练随堂演练课堂小结课堂小结三角形全等的判定方法判别方法条件结论作用课堂检测课堂检测已知:如图,在△ABC中,∠B=2C,∠AD是△ABC的角平分线,∠1=C,∠求证:AC=AB+CE1DEABCP41-练习1、2课后作业课后作业谢谢谢谢推进新课推进新课问题1先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B(即两角和它们的夹边分别相等).把画好的△A′B′C′剪下来,放到△ABC上,它们全等吗?探究“探究“ASA”ASA”判定方法判定方法知识点1探究DEA′B′C′...