三角函数的几何表示VIP免费

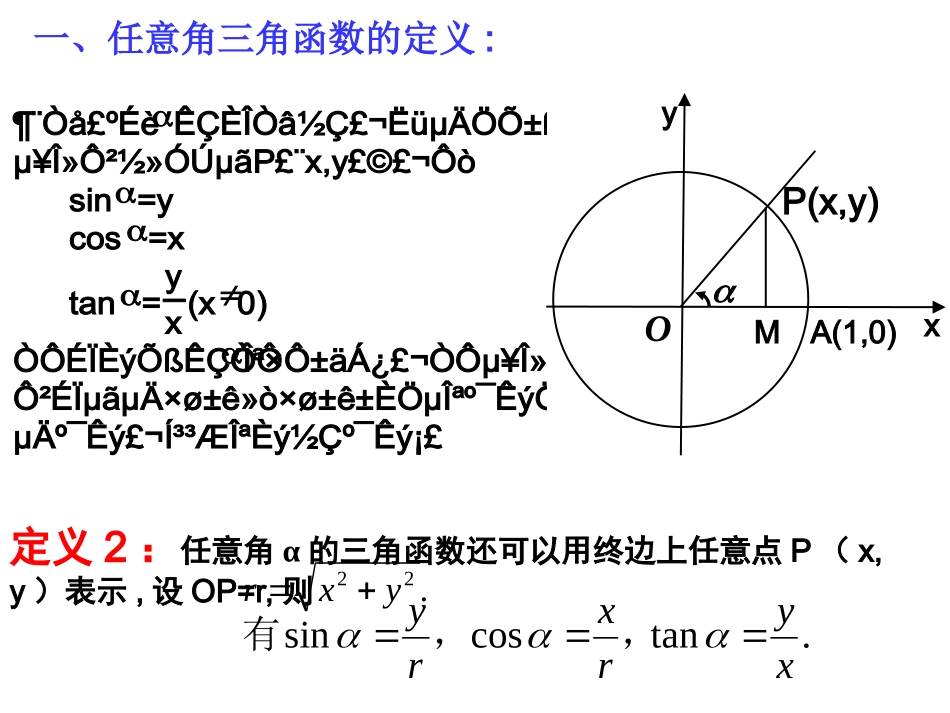
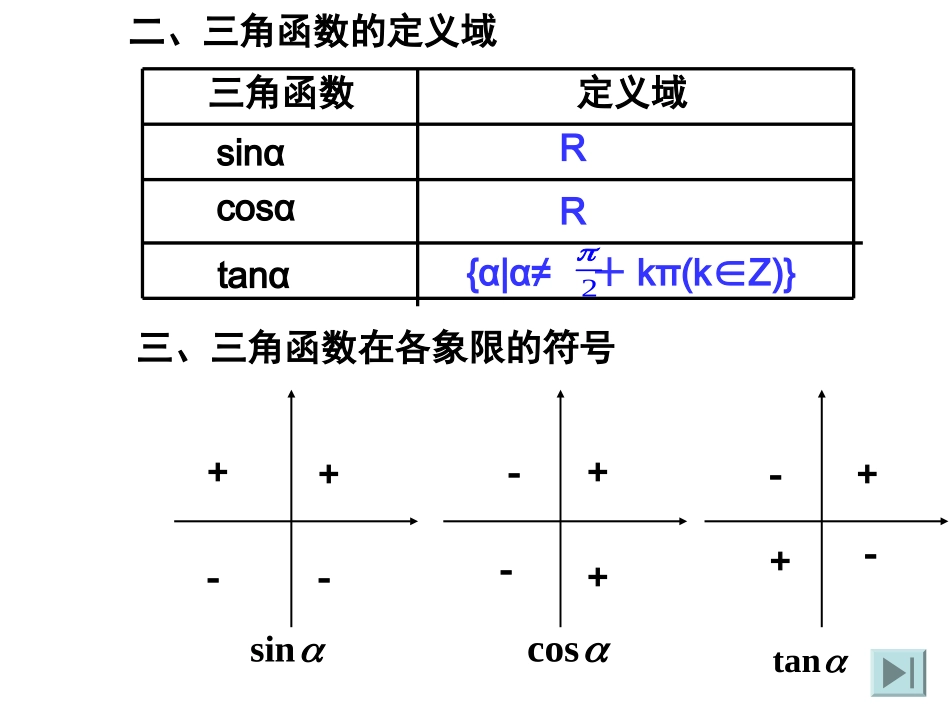
三角函数的几何表示OxyP(x,y)MA(1,0)一、任意角三角函数的定义:定义2：任意角α的三角函数还可以用终边上任意点P（x,y）表示,设OP=r,则.tancossinxyrxry，，有.22yxr¶¨Ò壺ÉèÊÇÈÎÒâ½Ç£¬ËüµÄÖÕ±ßÓ뵥λԲ½»ÓÚµãP£¨x,y£©£¬Ôòsin=ycos=xtan=yx(x0)ÒÔÉÏÈýÕßÊÇÒÔΪ×Ô±äÁ¿£¬ÒÔµ¥Î»Ô²ÉϵãµÄ×ø±ê»ò×ø±ê±ÈֵΪº¯ÊýÖµµÄº¯Êý£¬Í³³ÆΪÈý½Çº¯Êý¡£二、三角函数的定义域三角函数定义域sinαcosαtanαRR{α|α≠＋kπ(kZ)}∈2三、三角函数在各象限的符号sincostan++++++------α00300450600900180027003600弧度sinαcosαtanα064322300121212222232310-100-101331300不存在不存在,tan)2tan(,cos)2cos(,sin)2sin(kkk其中kZ∈终边相同的角的同一三角函数的值相等。一、背景知识任意角的三角函数是三角学中最基本最重要的概念之一。三角学起源于对三角形边角关系的研究，始于古希腊的喜帕恰斯、梅内劳斯和托勒密等人对天文的测量，在相当长的时期里隶属于天文学。直到1464年，德国数学家雷基奥蒙坦著《论各种三角形》，才独立于天文学之外对三角知识作了较系统的阐说；14~16世纪，三角学曾一度成为欧洲数学的主要内容，研究的方面包括三角函数值表的编制、平面三角形和球面三角形的解法，三角恒等式的建立和推导等等。1631年，三角学输入中国，三角学在中国早期比较通行的名称是“八线”和“三角”。“八线”是指在单位圆上的八种三角函数线：正弦线、余弦线、正切线、余切线、正割线、余割线、正矢线、余矢线。随着科学的发展，三角函数成为研究自然界和生产实践中周期变化现象的重要数学工具，它在测量、力学工程和无线电学中有着广泛的应用。任意角的三角函数是三角学中最基本最重要的概念之一。三角学起源于对三角形边角关系的研究，始于古希腊的喜帕恰斯、梅内劳斯和托勒密等人对天文的测量，在相当长的时期里隶属于天文学。直到1464年，德国数学家雷基奥蒙坦著《论各种三角形》，才独立于天文学之外对三角知识作了较系统的阐说；14~16世纪，三角学曾一度成为欧洲数学的主要内容，研究的方面包括三角函数值表的编制、平面三角形和球面三角形的解法，三角恒等式的建立和推导等等。1631年，三角学输入中国，三角学在中国早期比较通行的名称是“八线”和“三角”。“八线”是指在单位圆上的八种三角函数线：正弦线、余弦线、正切线、余切线、正割线、余割线、正矢线、余矢线。随着科学的发展，三角函数成为研究自然界和生产实践中周期变化现象的重要数学工具，它在测量、力学工程和无线电学中有着广泛的应用。探究：角是一个几何概念，同时角的大小也具有数量特征.我们从数的观点定义了三角函数，如果能从图形上找出三角函数的几何意义，就能实现数与形的完美统一.sinyMPcosxOMxyoMP(x,y)p(x,y)Mxop(x,y)xoxyoxyoMMMMppp正弦线余弦线思考：设α为锐角，你能根据正弦线和余弦线说明sinα＋cosα>1吗？POxyMMP＋OM>OP=1正切线正切线:AT:ATAT问题1：如图，设角α为第一象限角，其终边与单位圆的交点为P（x，y），则是正数，用哪条有向线段表示角α的正切值最合适？tanyxPOxyMOAATOMMPxytanATATPOxyMtanyATx正切线正切线问题2：若角α为第四象限角，其终边与单位圆的交点为P（x，y），则是负数，此时用哪条有向线段表示角α的正切值最合适？tanyxATATPOxyMtanyATx思考：若角α为第二象限角，其终边与单位圆的交点为P（x，y），则是负数，此时用哪条有向线段表示角α的正切值最合适？tanyxPOxyMATATtanyATxtanyx思考：若角α为第三象限角，其终边与单位圆的交点为P（x，y），则是正数，此时用哪条有向线段表示角α的正切值最合适？思考：根据上述分析，你能描述正切线的几何特征吗？过点A（1，0）作单位圆的切线，与角α的终边或其反向延长线相交于点T，则AT=tanα.ATOxyPATOxyP思考：当角α的终边在坐标轴上...