解二元一次方程组VIP免费

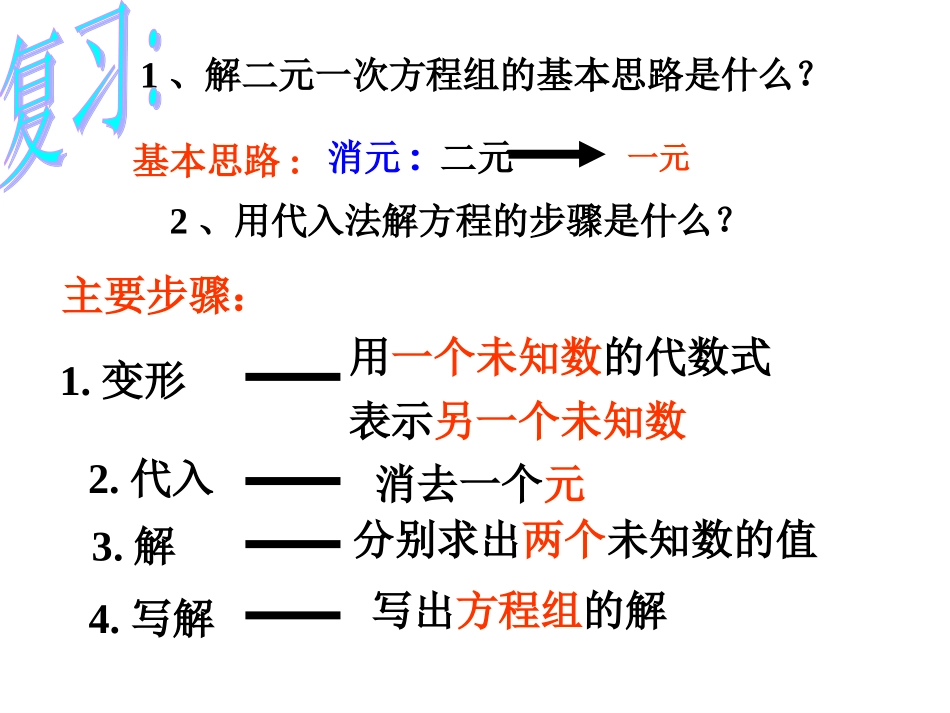
主要步骤：基本思路:4.写解3.解2.代入一元分别求出两个未知数的值写出方程组的解1.变形用一个未知数的代数式表示另一个未知数1、解二元一次方程组的基本思路是什么？2、用代入法解方程的步骤是什么？消去一个元消元:二元一元怎样解下面的二元一次方程组呢？11-52125y3xyx①②把②变形得：2115yx代入①，不就消去x了！小明11-52125y3xyx①②把②变形得1125xy可以直接代入①呀！小彬11-52125y3xyx①②和y5y5互为相反数……按按按按按按按按按按按按按按按按按按按小丽（3x＋5y）+（2x－5y）＝21+(－11)分析：11-52125y3xyx①②3X+5y+2x－5y＝10①左边+②左边=①右边+②右边5x＝10x=2所以原方程组的解是23xy11-52125y3xyx①②解:由①+②得:5x=10把x＝2代入①，得x＝2y＝3参考小丽的思路，怎样解下面的二元一次方程组呢？2x-5y=7①2x+3y=-1②观察方程组中的两个方程，未知数x的系数相等，都是2。把两个方程两边分别相减，就可以消去未知数x，同样得到一个一元一次方程。分析2x-5y=7①2x+3y=-1②解：把②－①得:8y＝－8y＝－1把y＝－1代入①，得2x－5×（－1）＝7解得:x＝1所以原方程组的解是x＝1y＝－1指出下列方程组求解过程中有错误步骤，并给予订正：7x－4y＝45x－4y＝－4解:①－②，得2x＝4－4，x＝0①①②②3x－4y＝145x＋4y＝2解①－②，得－2x＝12x＝－6解:①－②，得2x＝4＋4，x＝4解:①＋②，得8x＝16x＝2上面这些方程组的特点是什么?解这类方程组基本思路是什么？主要步骤有哪些？特点:基本思路:主要步骤：同一个未知数的系数相同或互为相反数加减消元:二元一元加减消去一个元求解分别求出两个未知数的值写解写出方程组的解A试一试7x-2y=39x+2y=-196x-5y=36x+y=-15用加减消元法解下列方程组.(你可以选择你喜欢的一题解答)例4.解方程组:1743123y2xyx①×3得所以原方程组的解是11xy①②分析：③-④得:y=2把y＝2代入①，解得:x＝3②×2得6x+9y=36③6x+8y=34④当方程组中两方程未知数系数不具备相同或互为相反数的特点时要建立一个未知数系数的绝对值相等的，且与原方程组同解的新的方程组。再用加减消元法解．分别相加y1.已知方程组x+3y=172x-3y=6两个方程就可以消去未知数分别相减2.已知方程组25x-7y=1625x+6y=10两个方程就可以消去未知数x一.填空题：只要两边只要两边练习二：用加减法解二元一次方程组。⑴7x-2y=39x+2y=-19⑵6x-5y=36x+y=-15做一做x=-1y=-5x=-2y=-31、若方程组的解满足2x-5y=-1，则m为多少？2、若(3x+2y-5)2+|5x+3y-8|=0求x2+y-1的值。x+y=8mx-y=2m1：总结：当两个二元一次方程中同一个未知数的系数相反或相等时，把两个方程的两边分别相加或相减，就能消去这个未知数，得到一个一元一次方程。这种方法叫做加减消元法，简称加减法。同减异加谈谈你对解二元一次方程组的认识请同学们归纳一下：什么样的方程组用“代入法”？什么样的方程组用“加减法”？二元一次方程一元一次方程消元转化主要步骤有哪些？加减消去一个元求解分别求出两个未知数的值变形同一个未知数的系数相同或互为相反数写解写出方程组的解你能把我们今天内容小结一下吗？1、本节课我们知道了用加减消元法解二元一次方程组的基本思路仍是“消元”。主要步骤是：通过两式相加（减）消去其中一个未知数。2、把求出的解代入原方程组，可以检验解题过程是否正确。