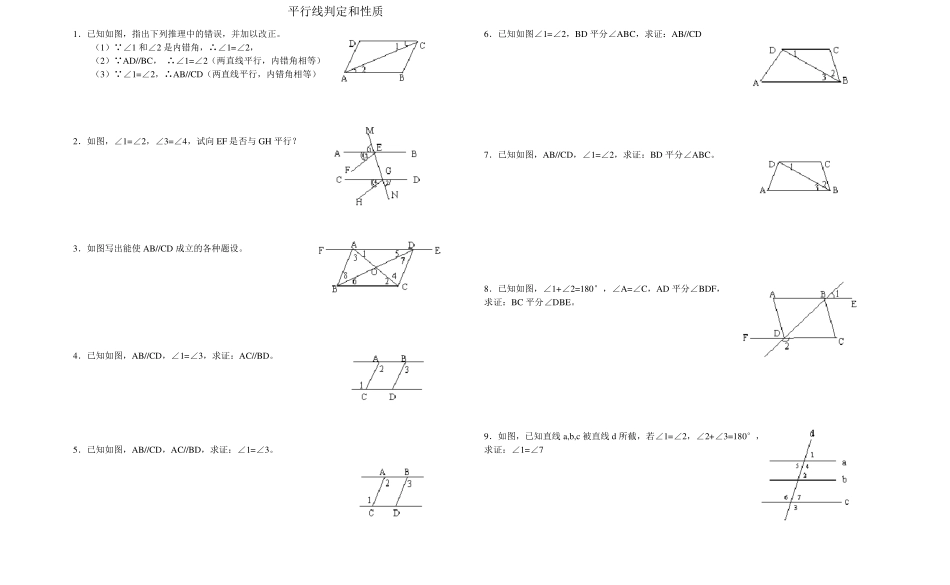
平行线判定和性质1.已知如图,指出下列推理中的错误,并加以改正。(1)∵∠1和∠2是内错角,∴∠1=∠2,(2)∵AD//BC,∴∠1=∠2(两直线平行,内错角相等)(3)∵∠1=∠2,∴AB//CD(两直线平行,内错角相等)2.如图,∠1=∠2,∠3=∠4,试向EF是否与GH平行?3.如图写出能使AB//CD成立的各种题设。4.已知如图,AB//CD,∠1=∠3,求证:AC//BD。5.已知如图,AB//CD,AC//BD,求证:∠1=∠3。6.已知如图∠1=∠2,BD平分∠ABC,求证:AB//CD7.已知如图,AB//CD,∠1=∠2,求证:BD平分∠ABC。8.已知如图,∠1+∠2=180°,∠A=∠C,AD平分∠BDF,求证:BC平分∠DBE。9.如图,已知直线a,b,c被直线d所截,若∠1=∠2,∠2+∠3=180°,求证:∠1=∠7三、证明角相等的基本方法第一章、第二章中已学过的关于两个角相等的命(1)同角(或等角)的余角相等;(2)同角(或等角)的补角相等;(3)对顶角相等;(4)两直线平行,同位角相等;内错角相等;同旁内角互补。10,如图∠1=∠2=∠C,求证∠B=∠C。11、已知如图,AB//CD,AD//BC,求证:∠A=∠C,∠B=∠D。12、已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,求证:∠1=∠2。四、两条直线位置关系的论证。两条直线位置关系的论证包括:证明两条直线平行,证明两条直线垂直,证明三点在同一直线上。1、学过证明两条直线平行的方法有两大类(一)利用角;(1)同位角相等,两条直线平行;(2)内错角相等,两条直线平行;(3)同旁内角互补,两条直线平行。(二)利用直线间位置关系:(1)平行于同一条直线的两条直线平行;(2)垂直于同一条直线的两条直线平行。13、如图,已知BE//CF,∠1=∠2,求证:AB//CD。14、如图CD⊥AB,EF⊥AB,∠1=∠2,求证:DG//BC。2、已经学过的证明两直线垂直的方法有如下二个:(1)两直线垂直的定义(2)一条直线和两条平行线中的一条垂直,这条直线也和另一条垂直。(即证明两条直线的夹角等于90o而得到。)15、如图,已知EF⊥AB,∠3=∠B,∠1=∠2,求证:CD⊥AB。五、一题多解。16、已知如图,∠BED=∠B+∠D。求证:AB//CD。