正弦定理及其应用VIP免费

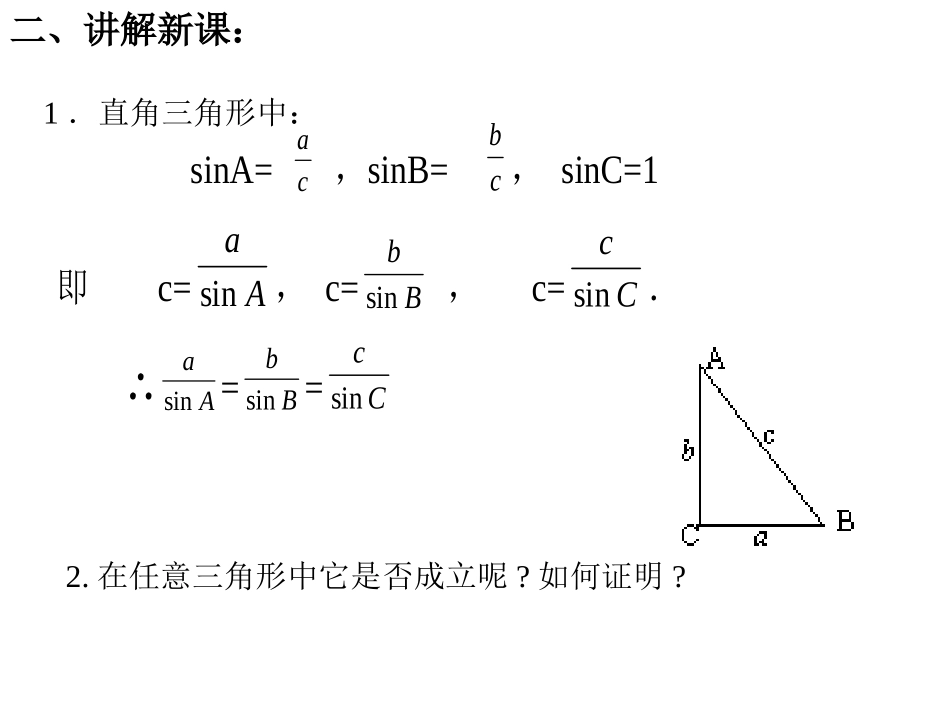
正弦定理及其应用一、引言：在直角三角形中，由三角形内角和定理、勾股定理、锐角三角函数，可以由已知的边和角求出未知的边和角。那么斜三角形怎么办？正弦定理、余弦定理我们可以利用黑龙江省绥化市第一中学陈洪波二、讲解新课：sinA=ca，sinB=cb，sinC=1即c=Aasin，c=Bbsin，c=Ccsin．∴Aasin=Bbsin=Ccsin1．直角三角形中：2.在任意三角形中它是否成立呢?如何证明?证明一：（向量法）过A作单位向量j垂直于AC由AC+CB=AB两边同乘以单位向量j得j•(AC+CB)=j•AB则j•AC+j•CB=j•AB∴|j|•|AC|cos90+|j|•|CB|cos(90C)=|j|•|AB|cos(90A)∴AcCasinsin∴Aasin=Ccsin同理，若过C作j垂直于CB得：Ccsin=Bbsin∴Aasin=Bbsin=Ccsin方法2:正弦定理：在任一个三角形中，各边和它所对角的正弦比相等，即AasinBbsinRCc2sin（R为△ABC外接圆半径）S△ABC=AbcBacCabsin21sin21sin21正弦定理的应用从理论上正弦定理可解决两类问题：1．两角和任意一边，求其它两边和一角；2．两边和其中一边对角，求另一边的对角，进而可求其它的边和角。（见图示）三、讲解范例：例1已知在BbaCAcABC和求中，,,30,45,1000由CcBbsinsin得25654262075sin2030sin105sin10sinsin000CBcb解：0030,45,10CAc∴00105)(180CAB由CcAasinsin得21030sin45sin10sinsin00CAca例2在CAacBbABC,,1,60,30和求中，00090,30,,60,ACCBCBcb为锐角，∴222cba解：∵21360sin1sinsin,sinsin0bBcCCcBb例3CBbaAcABC,,2,45,60和求中，或0060,75,13CBb00120,15,13CBb解：23245sin6sinsin,sinsin0aAcCCcAa0012060,或Cca1360sin75sin6sinsin,75600000CBcbBC时，当1360sin15sin6sinsin,151200000CBcbBC时，当1Aa7,b14,A30,Ba30,b25,A150,a6,b9,A45,Db9,c10,B60,C、下列判断中正确的是（）、有两解、有一解、有两解、无解B四、课堂练习：2.在△ABC中，kCcBbAasinsinsin,则k为()A.2RB.RC.4RD.R21(R为△ABC外接圆半径)3.△ABC中，sin2A=sin2B+sin2C，则△ABC为()A.直角三角形B.等腰直角三角形C.等边三角形D.等腰三角形AA4.在△ABC中，求证：2222112cos2cosbabBaA2222sin21sin21bBaA－－左＝222222sin21sin21bBbaAa右2211ba思考：已知△ABC，BＤ为B的平分线，求证：AB∶BC＝AＤ∶ＤCDBCDCBDCBCABDADADBABsinsin,sinsin提示：