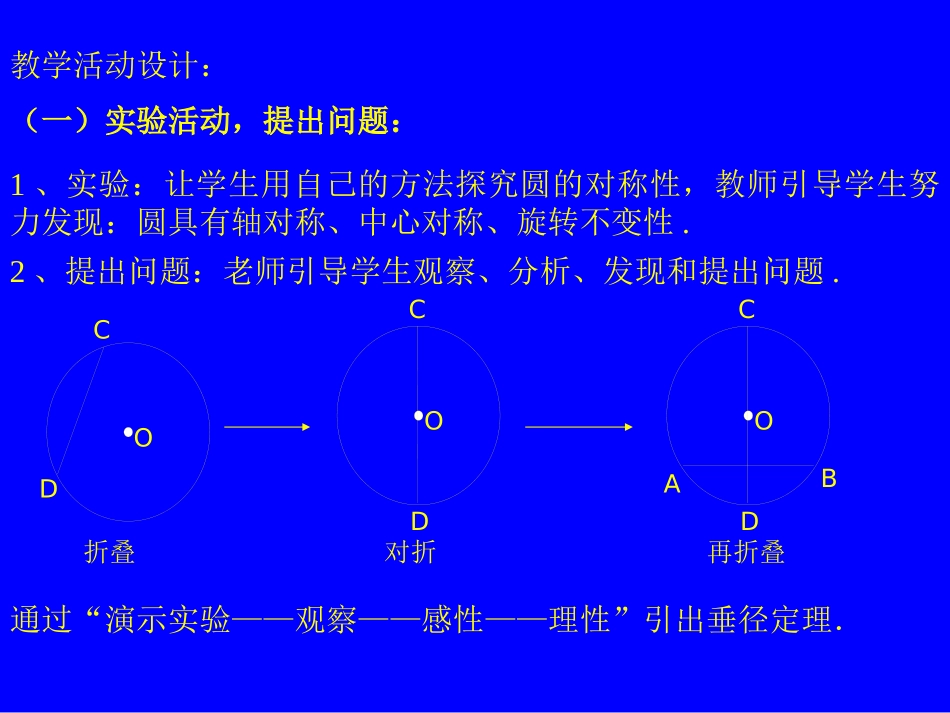
第七章圆第三节垂直于弦的直径(一)教学目标:(1)理解圆的轴对称性及垂径定理的推证过程;能初步应用垂径定理进行计算和证明;(2)进一步培养学生观察问题、分析问题和解决问题的能力;(3)通过圆的对称性,培养学生对数学的审美观,并激发学生对数学的热爱.教学重点和难点:重点:(1)垂径定理及应用;(2)从感性到理性的学习能力.难点:垂径定理的证明.教学活动设计:(一)实验活动,提出问题:1、实验:让学生用自己的方法探究圆的对称性,教师引导学生努力发现:圆具有轴对称、中心对称、旋转不变性.2、提出问题:老师引导学生观察、分析、发现和提出问题.OABCDCDOCDO对折再折叠折叠通过“演示实验——观察——感性——理性”引出垂径定理.(二)垂径定理及证明已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E.AC=BC,AD=DB.求证:AE=EB,ACDBOE(三)应用和训练例1、如图,已知在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.ABOE例2、已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点.求证:AC=BD.OACDB(四)小节与反思教师组织学生进行:知识:(1)圆的轴对称性;(2)垂径定理及应用.方法:(1)垂径定理和勾股定理有机结合计算弦长、半径、弦心距等问题的方法,构造直角三角形;(2)在因中解决与弦有关问题经常作的辅助线——弦心距;(3)为了更好理解垂径定理,一条直线只要满足①过圆心;②垂直于弦;则可得③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧.(五)作业教材P84中11、12、13.