2.2.1函数的单调性VIP免费

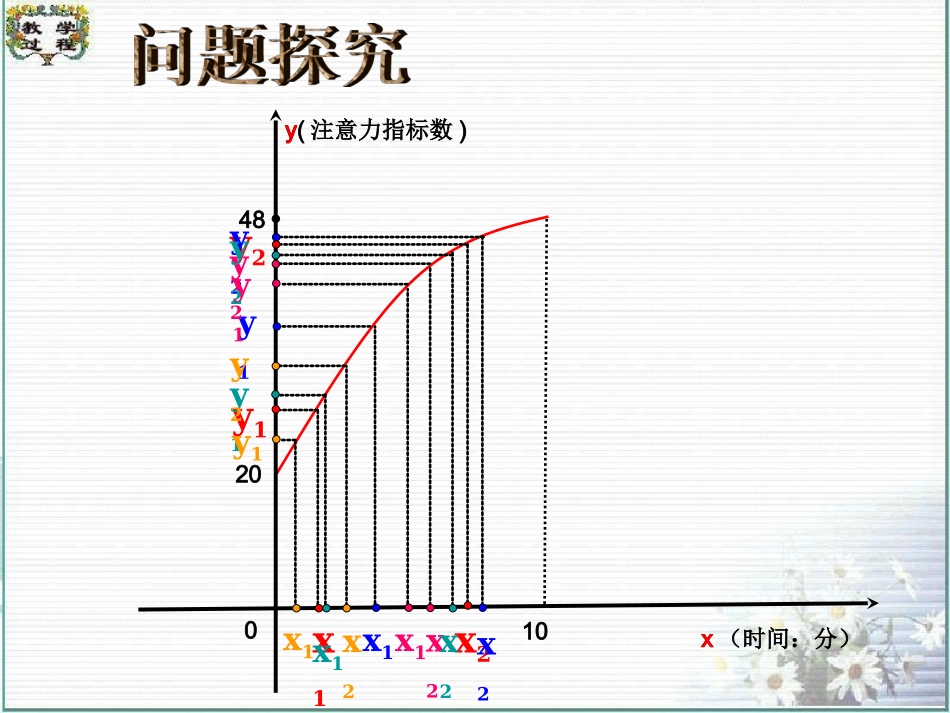
通过实验研究，专家发现：中学生听课的注意力指标是随着老师讲课时间的变化而变化的。讲课开始时，学生的兴趣激增，中间有一段时间，学生的兴趣保持平稳的状态，随后开始分散。学生注意力指标数随时间变化的函数图象如图所示（指标数越大表示学生注意力越集中）。——摘自2004年“TRULY信利杯”全国数学竞赛试题第11题483920x（时间：分）y(指标数)05102045x（时间：分）y(注意力指标数)02010204548。请你说出注意力指标数与时间在［0，45］内的变化规律.x（时间：分）0201048y(注意力指标数)xyx1x2y1y2x1x2y1y2x1x2y1y2x1x2y1y2x1x2y1y2一般地，设函数y=f(x)定义域为A，区间如果对于区间I内的任意两个值x1、x2，当x1f(x2)，那么就说y=f(x)在区间I上是单调减函数此时，I称为y=f(x)的单调减区间任意x1f(x2)如果函数y=f(x)在区间I上是单调增函数或单调减函数，那么就说函数y=f(x)在区间I上具有单调性.单调增区间和单调减区间统称为单调区间.都有都有x（时间：分）y(注意力指标数)02010204548。x（时间：分）y(注意力指标数)02010204548。苏教版普通高中课程标准实验教科书（必修）第一册苏教版普通高中课程标准实验教科书（必修）第一册函数的单调性函数的单调性,,21xx在给定区间上任取21xx)f(x)f(x21函数f(x)在给定区间上为增函数。Oxy)x(fy如何用x与f(x)来描述上升的图象？)x(f11x如何用x与f(x)来描述下降的图象？,,21xx在给定区间上任取21xx函数f(x)在给定区间上为减函数。)f(x)f(x21)x(f1)x(f2)x(fyOxy1x2x)x(f22x(1)定义在R上的函数f(x)满足f(2)>f(1)，则函数f(x)是R上的增函数.()(2)函数f(x)是R上的增函数,则必有f(2)>f(1).()(3)定义在R上的函数f(x)满足f(2)>f(1)，则函数f(x)在R上不是减函数.()×√辨一辨：√(4)若定义在R上的函数f(x)在区间上是单调递增函数，在区间上也是单调递增函数，则函数f(x)在R上是单调增函数.()(,0][0,)(5)若定义在R上的函数f(x)在区间上是单调递增函数，在区间上也是单调递增函数，则函数f(x)在R上是单调增函数.()(,0](0,)辨一辨：×√Oxy2x2y21yOxx1yOxy1xy1-1yOx2xy写出下列函数的单调区间：例1下图是定义在[－5，5]上的函数y＝f（x）的图象，根据图象说出y＝f（x）的单调区间，以及在每一单调区间上，y＝f（x）是增函数还是减函数.解：y＝f（x）的单调区间有[－5，－3），[－3，1）[1，3），[3，5].其中y＝f（x）在[－5，－3），[1，3）上是减函数，在[－3，1），[3，5）上是增函数.xyo31-35-5数学应用例2证明函数f(x)=2x+1在区间(-∞,+∞)上是增函数。注意：我们在证明函数的单调性时，不能“以图代证”,而是严格按照定义证明.回想一下,定义的本质是什么?本题怎样用定义来证明?内任意是区间设),(x,x21)x2(x)1x2()1x2()x(f)x(f2121210xx,xx21210)x(f)x(f21)x(f)x(f21即),(1x2)x(f在区间则函数证明：。两个实数，且xx21是增函数。例2证明函数f(x)=2x+1在区间(-∞,+∞)上是增函数。证明函数单调性的步骤：第一步：取值.即任取区间内的两个值，且x1f(x2)所以f(x)=－x3+1在(－∞,+∞)上是减函数.课本P.40第2、6、7题