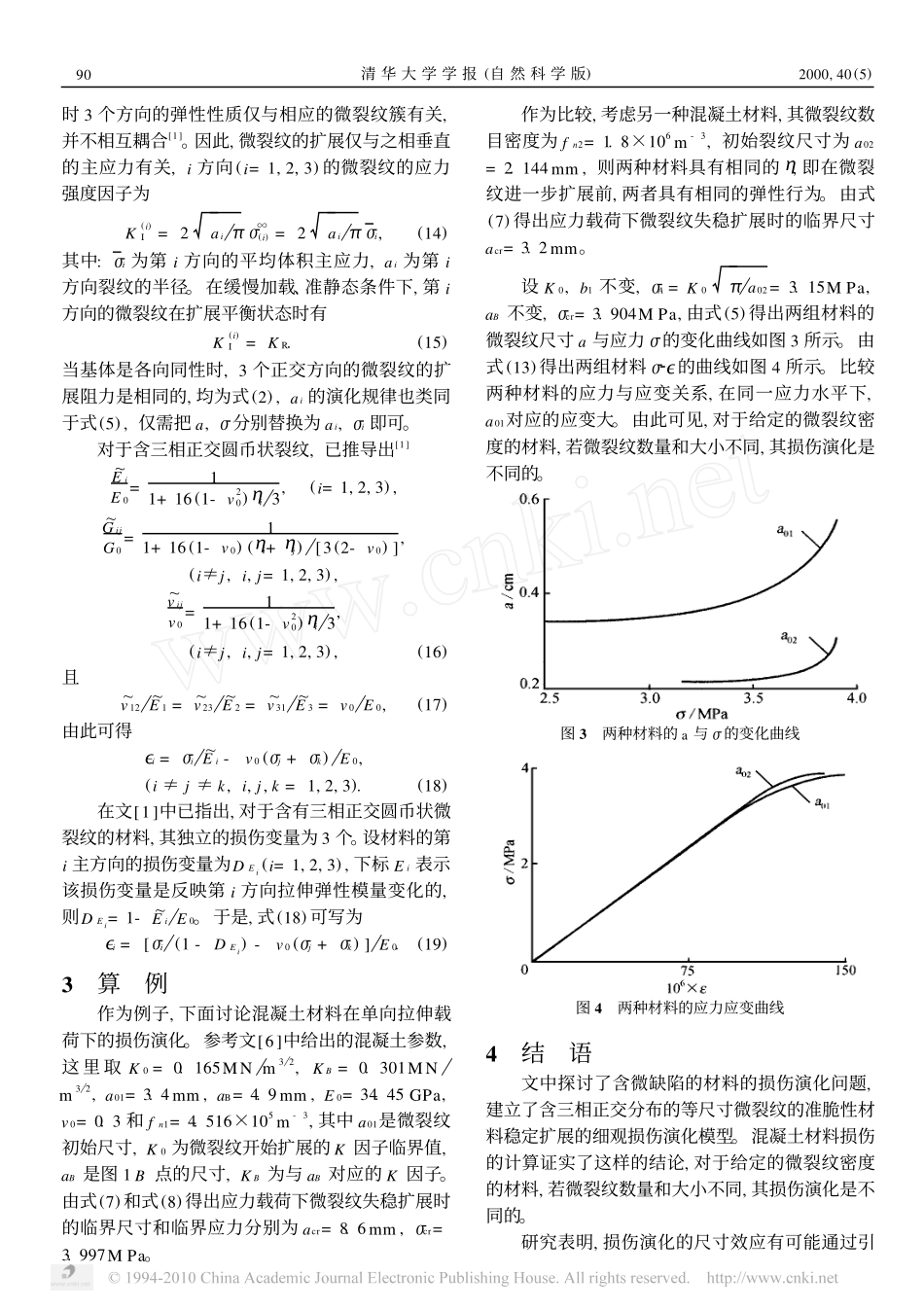
ISSN100020054CN1122223�N清华大学学报(自然科学版)JTsinghuaUniv(Sci&Tech),2000年第40卷第5期2000,Vol.40,No.524�348891准脆性材料的细观损伤演化模型3赵爱红,虞吉林(中国科学技术大学力学和机械工程系,合肥230027)收稿日期:1999209213作者简介:赵爱红(19602),女(汉),山东,副教授(现工作单位:清华大学精仪系摩擦学国家重点实验室)3基金项目:中国科学院“九五”基础性研究重大项目(KJ951212201)文摘:针对以缺陷密度为参量的细观损伤演化模型的局限性,着重研究了微裂纹尺寸对损伤演化的影响。提出了含三相正交分布等尺寸微裂纹的准脆性材料稳定扩展的细观损伤演化模型。给出了微裂纹特征尺寸随应力变化的显式表达式,并由此得到了含微裂纹的准脆性材料损伤本构关系。通过实例,对初始含有相同密度、不同尺寸和数量的微裂纹的两种混凝土材料在单向拉伸载荷下的损伤演化进行了数值计算和比较。结果证实:含大尺寸微裂纹的材料损伤发展较快,相应地,加载到同一应力水平时,具有较大的应变。关键词:准脆性材料;细观损伤演化;尺寸效应;微裂纹稳定扩展中图分类号:O346.5文献标识码:A文章编号:100020054(2000)0520088204损伤演化是材料损伤研究的难点和重点,目前仍不成熟。其研究方法主要有两种,一是在热力学框架下,提出以实验为基础的经验损伤演化规律;二是考虑材料的细观结构,将断裂力学、细观力学、弹塑性分析方法应用于微裂纹、微孔洞的形核、扩展,从而建立材料的损伤演化规律。后者比前者更接近于材料损伤演化的物理过程,但却存在一些局限性。事实上,材料损伤的演化往往取决于多个细观结构参数及其极端值,如微裂纹的尺寸、排列方式和间距等。其中,微裂纹尺寸对材料损伤演化起重要作用。因此,一个合理的细观损伤模型必须包含有微尺度参量。本文在以微缺陷密度为细观参量的细观损伤表征模型[1]的基础上,提出了含三相正交分布等尺寸微裂纹的准脆性材料的细观损伤演化模型。以断裂力学、细观力学的方法,建立了微裂纹稳定扩展的演化规律和材料损伤本构方程。计算比较了初始含相同密度、不同大小和数量的微裂纹的两种混凝土材料在单向拉伸载荷下的损伤演化,建立了一个考虑含微缺陷尺度效应的损伤本构关系。1一维损伤演化模型准脆性材料典型的应力应变曲线如图1所示。从实验观测可知,OA段为未损伤的线弹性阶段,这一阶段仅存在初始的微裂纹,并不扩展。AC段为损伤均匀扩展阶段,B点是AC段任意一点(下面例题中用到),D点以后,出现损伤局部化,D点的位置与材料内部的初始缺陷分布的均匀性有关。在载荷控制的加载条件下,C点以后材料失稳。但在位移控制的加载条件下,C点以后,材料仍是稳定的,直至D点。图1准脆性材料的应力应变曲线下面研究载荷控制的加载条件下的损伤稳定扩展阶段。设材料内含有平行的圆币状微裂纹,受到与之垂直方向上平均应力Ρ的单向拉伸载荷。忽略应力场和材料在细观层次上的不均匀性,某一微裂纹的应力强度因子可表示为K1=2a�ΠΡ∞,(1)其中Ρ∞为某一微裂纹无穷远处的、与微裂纹相垂直的正应力,它受其他各微裂纹存在及扩展的影响。进一步假设材料代表体元(representativevolumeelement,RVE)内所有微裂纹所受的力是相同的,等于RVE的平均应力,即Ρ∞=Ρ。Ρ已由文[1]按Mori2Tanaka方法求出。以下为了简化,将Ρ均简写为Ρ。对于存在宏观裂纹的固体,在小尺度屈服条件下,断裂力学已成功地用于处理裂纹扩展问题。一般认为,对脆性材料,当应力强度因子达到某一临界值时,裂纹便失稳扩展,而对于韧性材料,存在一条裂纹扩展阻力曲线即R曲线[2]以及相应的稳定扩展阶段。图2为在载荷控制实验中的裂纹阻力曲线和裂纹驱动力曲线。由于缺乏实验数据,微裂纹的扩展规律是一个尚不清楚的问题。但是,即使对于脆性很好的材料,在微裂纹的扩展过程中,微裂纹尖端附近也存在着复杂的能量耗散机制,如细观塑性变形、微孔洞的形核等[3,4]。考虑到裂端非线性区的大小已可与微裂纹本身的尺度相比较,假设微裂纹的扩展也存在一条如图2所示的R曲线。图2裂纹阻力曲线和裂纹驱动力曲线示意图设扩展阻力KR与微裂纹的尺寸a的关系为KR=K0+b1a-a0,(2)其中:KR是以应力强度因子标志法表示的R曲线,a0为微裂纹的初始尺寸,K0为微裂...