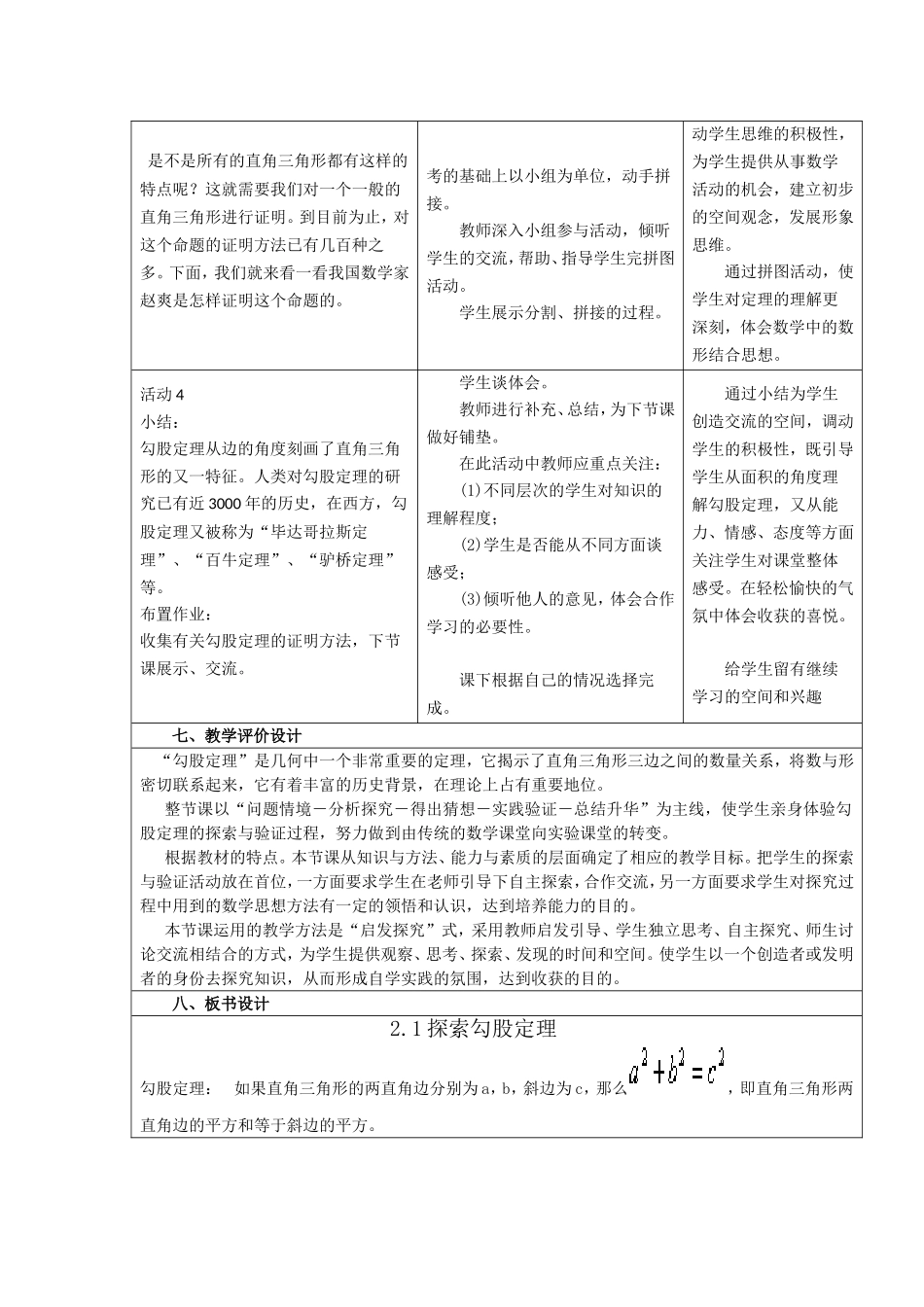
《勾股定理》教学设计课题:勾股定理科目数学教学对象八年级学生课时1课时提供者王志芳单位山西省平遥县朱坑三中一、教学目标知识与技能目标:培养正确的观察事物分析事物能力,理解并掌握勾股定理及其证明过程与方法目标:在学生经历“观察—猜想—归纳—验证”勾股定理的过程中,发展合情推理能力,体会数形结合和从特殊到一般的思想情感与态度目标:通过对勾股定理历史的了解,感受数学文化,激发学习兴趣;在探究活动中,培养学生的合作交流意识和探索精神二、教学内容分析了解勾股定理的文化背景,体验勾股定理的探索过程。在勾股定理的探索过程中,发展合情推理能力,体会数形结合的思想。三、学情分析大部分同学学习积极性尚可,能较好地完成学习任务,但很多学生学习习惯不是很好,整体水平不均,学习比较浮躁,这主要表现在课堂纪律和作业质量方面。一、学习状态绝大部分同学都能跟上现有的进度,上课发言尚积极,个别同学表现的还比较出色,但也有部分同学的理解能力和接受能力不尽人意,学习成绩极不理想。从课堂上看,他们的注意力不能长时间集中,很容易分心,作业和试卷上的错误比较多,对于老师的问题一问三不知,在今后的教学过程中对这些孩子要特别注意。二、学习习惯部分学生有主动学习的行为,深得老师赞赏。比较喜欢上数学课,学习热情也很高,并喜欢与老师友好相处,同学之间、师生之间常在一起交流学习体会。但仍有少部分学生学习懒散、学习习惯差,如:粗心大意、书写不认真,不愿思考问题,上课开小差,依赖老师讲解,依赖同学的帮助,有些学生抄作业现象比较严重。四、教学策略选择与设计通过拼图活动,体验数学思维的严谨性,发展形象思维。在探究活动中,学会与人合作并能与他人交流思维的过程和探究的结果。五、教学重点及难点重点:探索和证明勾股定理难点:用拼图方法证明勾股定理六、教学过程(这一部分是该教学设计方案的关键所在,在这一部分,要说明教学的环节及所需的资源支持、具体的活动及其设计意图以及那些需要特别说明的教师引导语)教师活动学生活动设计意图活动12002年在北京召开了第24届国际数学家大会,它是最高水平的全球性数教师出示照片及图片。学生观察图片发表见解。教师做补充说明:这个图案是我国汉代数学从现实生活中提出“赵爽弦图”,为学生能够积极主动地投学科学学术会议,被誉为数学界的“奥运会”。这就是本届大会会徽的图案。(1)你见过这个图案吗:(2)你听说过“勾股定理”吗?家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”。在本次活动中,教师应重点关注:(1)学生对“赵爽弦图”及勾股定理的历史是否感兴趣;(2)(2)学生对勾股定理的了解程度。入到探索活动创设情境,激发学生学习热情。同时为探索勾股定理提供背景材料。活动2毕达哥拉斯是古希腊著名的数学家。相传在2500年以前,他在朋友家做客时,发现朋友家用地砖铺成的地面反映了直角三农角型的某种特性。(1)现在请你也观察一下,你能有什么发现吗?(2)等腰直角三角形是特殊的直角三角形,一般的直角三角形是否也有这样的特点呢?(3)你有新的结论吗?教师展示图片并提出问题。学生观察图片,分组交流。教师引导学生总结:等腰直角三角形的两条直角边平方的和等于斜边的平方。在独立探究的基础上,学生分组交流。教师参与小组活动,指导、倾听学生交流。针对不同认识水平的学生,引导其用不同的方法得出大正方形的面积。在本次活动中,教师应重点关注:1.给学生留出充分的时间思考和交流,鼓励学生大胆说出自己的看法;2.学生能否准确挖掘出图形中的隐含条件,计算各个正方形的面积;3.学生能否用不同方法得到大正方形的面积(先补全再分割、旋转),引导学生重点学习赵爽弦图的分割方法;4.学生能否将三个正方形面积的关系转化为直角三角形三条边之间的关系,并用自己的语言叙述出来;5.学生能否主动参与探究活动,在讨论中发表自己的见解,倾听他人的意见,对不同的观点进行质疑,从中获益。问题是思维的起点,通过问题激发学生好奇、探究和主动学习的欲望。渗透从特殊到一般的数学思想,为学生提供参与数学活动的时间和空间,发挥学生的主体作用;培养学生的...