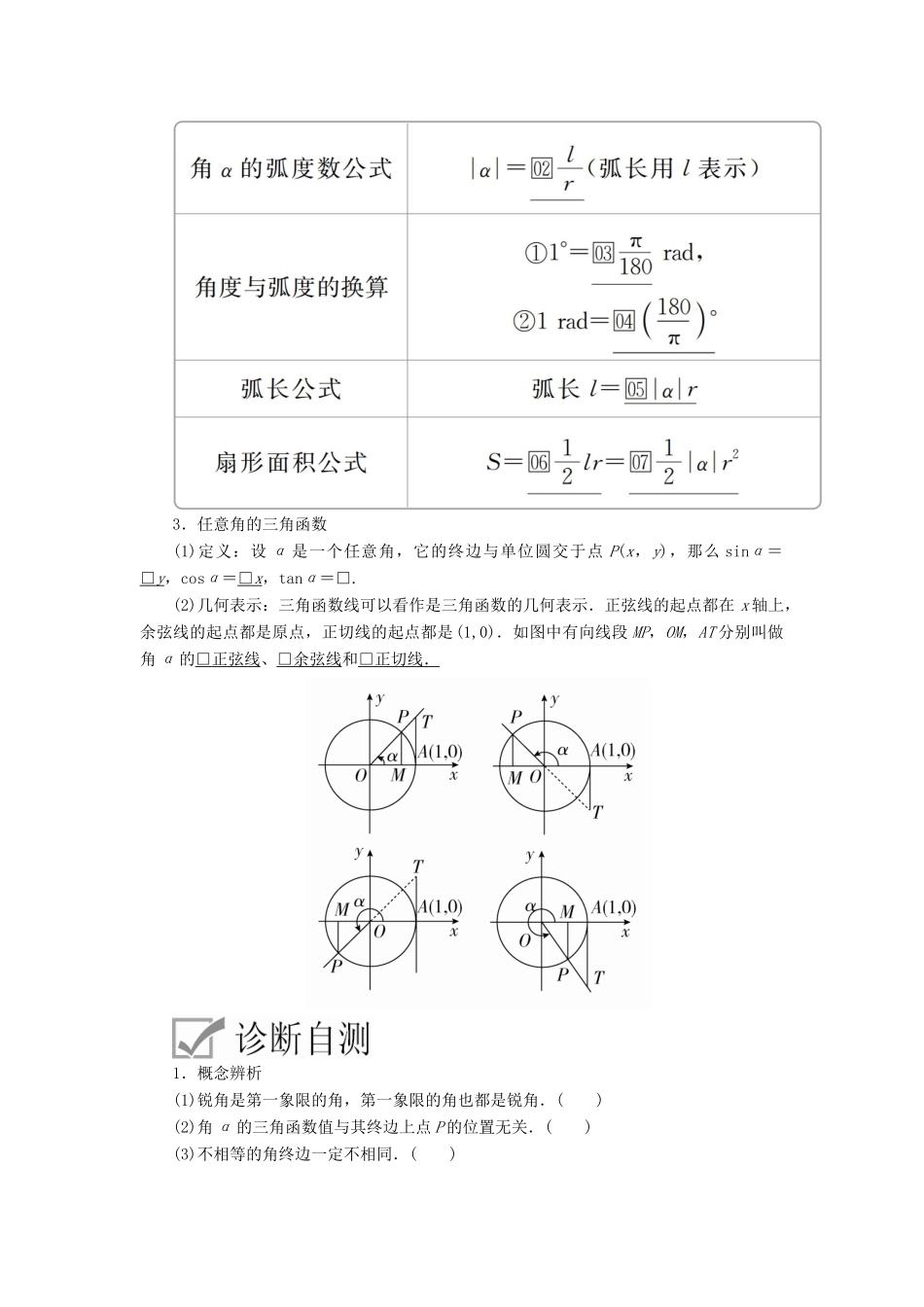
第三章三角函数、解三角形第1讲任意角和弧度制及任意角的三角函数1.任意角的概念(1)定义:角可以看成平面内的一条射线绕着□端点从一个位置旋转到另一个位置所成的图形.(2)角的分类(3)终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z}.2.弧度制的定义和公式(1)定义:把长度等于□半径长的弧所对的圆心角叫做1弧度的角.正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.(2)公式3.任意角的三角函数(1)定义:设α是一个任意角,它的终边与单位圆交于点P(x,y),那么sinα=□y,cosα=□x,tanα=□.(2)几何表示:三角函数线可以看作是三角函数的几何表示.正弦线的起点都在x轴上,余弦线的起点都是原点,正切线的起点都是(1,0).如图中有向线段MP,OM,AT分别叫做角α的□正弦线、□余弦线和□正切线.1.概念辨析(1)锐角是第一象限的角,第一象限的角也都是锐角.()(2)角α的三角函数值与其终边上点P的位置无关.()(3)不相等的角终边一定不相同.()(4)借助三角函数线可知,若α为第一象限角,则sinα+cosα>1.()答案(1)×(2)√(3)×(4)√2.小题热身(1)下列与的终边相同的角的表达式中正确的是()A.2kπ+45°(k∈Z)B.k·360°+(k∈Z)C.k·360°-315°(k∈Z)D.kπ+(k∈Z)答案C解析角度制与弧度制不能混用,排除A,B;因为=2π+,所以与终边相同的角可表示为k·360°+45°(k∈Z)或k·360°-315°等,故选C.(2)若角θ同时满足sinθ<0且tanθ<0,则角θ的终边一定落在()A.第一象限B.第二象限C.第三象限D.第四象限答案D解析因为sinθ<0,所以θ的终边位于x轴的下方,因为tanθ<0,所以θ的终边在第二、四象限,所以角θ的终边一定落在第四象限.(3)已知扇形的圆心角为120°,其弧长为2π,则此扇形的面积为________.答案3π解析设此扇形的半径为r,由题意得r=2π,所以r=3,所以此扇形的面积为×2π×3=3π.(4)设角θ的终边经过点P(4,-3),那么2cosθ-sinθ=________.答案解析因为r=|OP|==5,所以cosθ=,sinθ=-,所以2cosθ-sinθ=2×-=.题型象限角与终边相同的角1.(2018·长春一模)若角α的顶点为坐标原点,始边在x轴的非负半轴上,终边在直线y=-x上,则角α的取值集合是()A.{αB.{αC.{αD.{α答案D解析因为直线y=-x的倾斜角是,所以终边落在直线y=-x上的角的取值集合为{α,故选D.2.与2019°的终边相同,且在0°~360°内的角是________.答案219°解析因为2019°=5×360°+219°,所以与2019°终边相同的角可表示为k·360°+219°(k∈Z).其中在0°~360°内的角是219°.3.若角α是第二象限角,则是第________象限角.答案一或三解析因为角α是第二象限角,所以2kπ+<α<2kπ+π,k∈Z,所以kπ+<