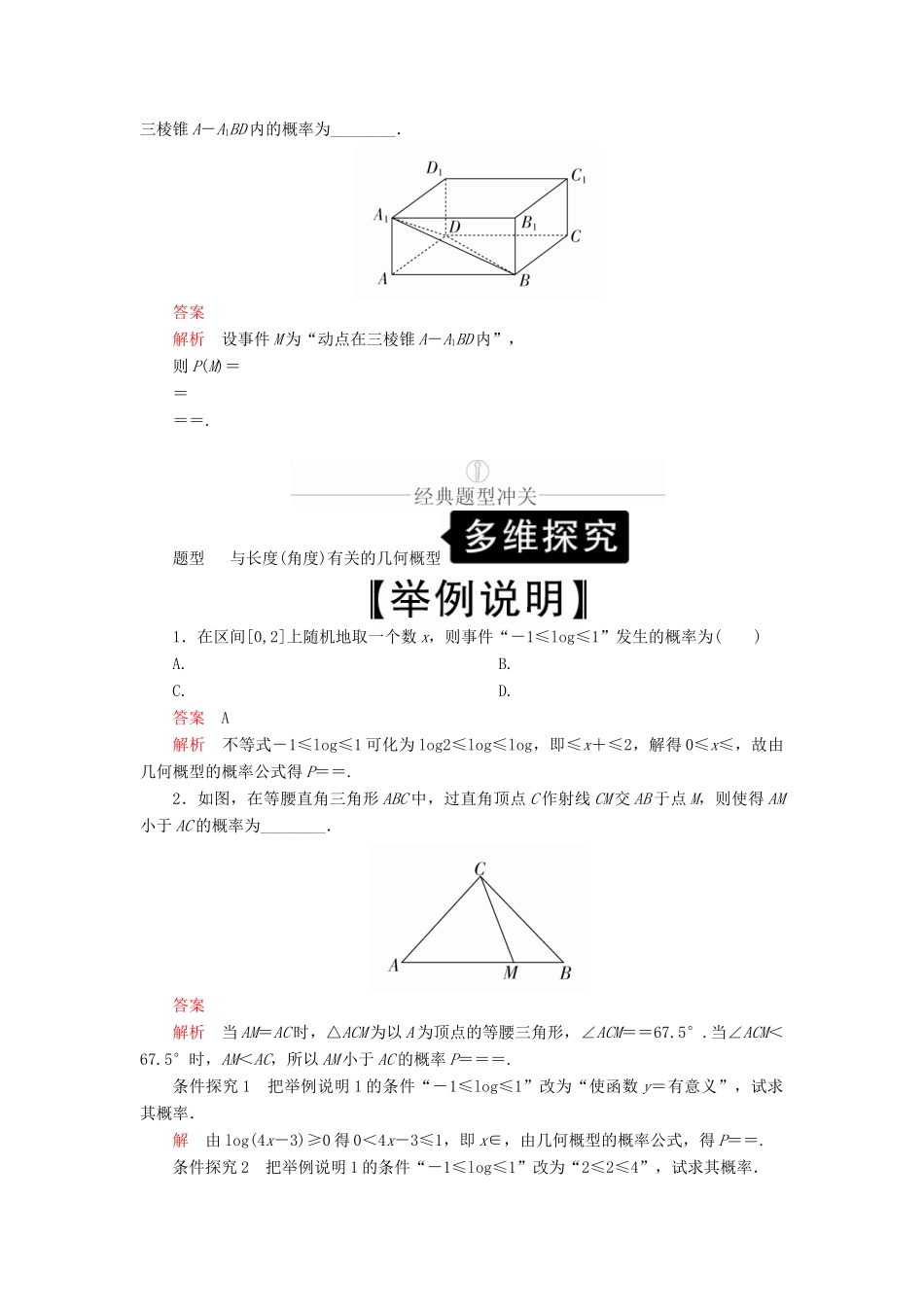
第6讲几何概型[考纲解读]1.了解随机数的意义,能运用模拟方法估计概率.2.了解几何概型的意义,并能求与长度或面积有关的几何概型的概率.(重点)[考向预测]从近三年高考情况来看,本讲是高考的热点之一.预测2020年将会考查:①与长度有关的几何概型,常与函数、不等式、向量结合;②与面积有关的几何概型,常涉及线性规划、定积分等内容.题型为客观题,试题难度不大,属中、低档试题.1.几何概型的定义如果每个事件发生的概率只与构成该事件区域的□长度(面积或体积)成比例,那么称这样的概率模型为几何概率模型,简称几何概型.2.几何概型的两个基本特点3.几何概型的概率公式P(A)=□.1.概念辨析(1)随机模拟方法是以事件发生的频率估计概率.()(2)与面积有关的几何概型的概率与几何图形的形状有关.()(3)几何概型中,每一个基本事件就是从某个特定的几何区域内随机地取一点,该区域中的每一点被取到的机会相等.()(4)在几何概型定义中的区域可以是线段、平面图形、立体图形.()答案(1)√(2)×(3)√(4)√2.小题热身(1)有四个游戏盘,将它们水平放稳后,在上面扔一个玻璃小球,若小球落在阴影部分,则可中奖,小明要想增加中奖机会,应选择的游戏盘是()答案A解析如题干选项中图,各种情况的概率都是其面积比,中奖的概率依次为P(A)=,P(B)=,P(C)=,P(D)=,所以P(A)>P(C)=P(D)>P(B).故选A.(2)(2016·全国卷Ⅰ)某公司的班车在7:30,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是()A.B.C.D.答案B解析解法一:7:30的班车小明显然是坐不到的.当小明在7:50之后8:00之前到达,或者8:20之后8:30之前到达时,他等车的时间将不超过10分钟,故所求概率为=.故选B.解法二:当小明到达车站的时刻超过8:00,但又不到8:20时,等车时间将超过10分钟,7:50~8:30的其他时刻到达车站时,等车时间将不超过10分钟,故等车时间不超过10分钟的概率为1-=.故选B.(3)如图所示,在直角坐标系内,射线OT落在30°角的终边上,任作一条射线OA,则射线OA落在∠yOT内的概率为________.答案解析根据题图,因为射线OA在坐标系内是等可能分布的,所以OA落在∠yOT内的概率为=.(4)如图,在长方体ABCD-A1B1C1D1中,有一动点在此长方体内随机运动,则此动点在三棱锥A-A1BD内的概率为________.答案解析设事件M为“动点在三棱锥A-A1BD内”,则P(M)====.题型与长度(角度)有关的几何概型1.在区间[0,2]上随机地取一个数x,则事件“-1≤log≤1”发生的概率为()A.B.C.D.答案A解析不等式-1≤log≤1可化为log2≤log≤log,即≤x+≤2,解得0≤x≤,故由几何概型的概率公式得P==.2.如图,在等腰直角三角形ABC中,过直角顶点C作射线CM交AB于点M,则使得AM小于AC的概率为________.答案解析当AM=AC时,△ACM为以A为顶点的等腰三角形,∠ACM==67.5°.当∠ACM<67.5°时,AM<AC,所以AM小于AC的概率P===.条件探究1把举例说明1的条件“-1≤log≤1”改为“使函数y=有意义”,试求其概率.解由log(4x-3)≥0得0<4x-3≤1,即x∈,由几何概型的概率公式,得P==.条件探究2把举例说明1的条件“-1≤log≤1”改为“2≤2≤4”,试求其概率.解由2≤2≤4得1≤x+≤2,即x∈,由几何概型的概率公式,得P==.1.与长度有关的几何概型(1)如果试验结果构成的区域的几何度量可用长度表示,则其概率的计算公式为P(A)=.(2)与时间、不等式及其解有关的概率问题与时间、不等式及其解有关的概率问题可依据转化与化归思想将其转化为与长度有关的几何概型,利用几何概型求解.2.与角度有关的几何概型当涉及射线的转动,扇形中有关落点区域问题时,应以角的大小作为区域度量来计算概率,且不可用线段的长度代替,这是两种不同的度量手段.1.已知函数f(x)=-x3+3x2,在区间(-2,5)上任取一个实数x0,则f′(x0)≥0的概率为________.答案解析因为f′(x)=-3x2+6x=-3x(x-2),所以由f′(x0)≥0,解得0≤x0≤2.由几何概型的概率计算公式得f′(x0)≥0的概率P==.2.如图,四边形ABCD为矩形,AB=,BC=1,以A为圆心,1...