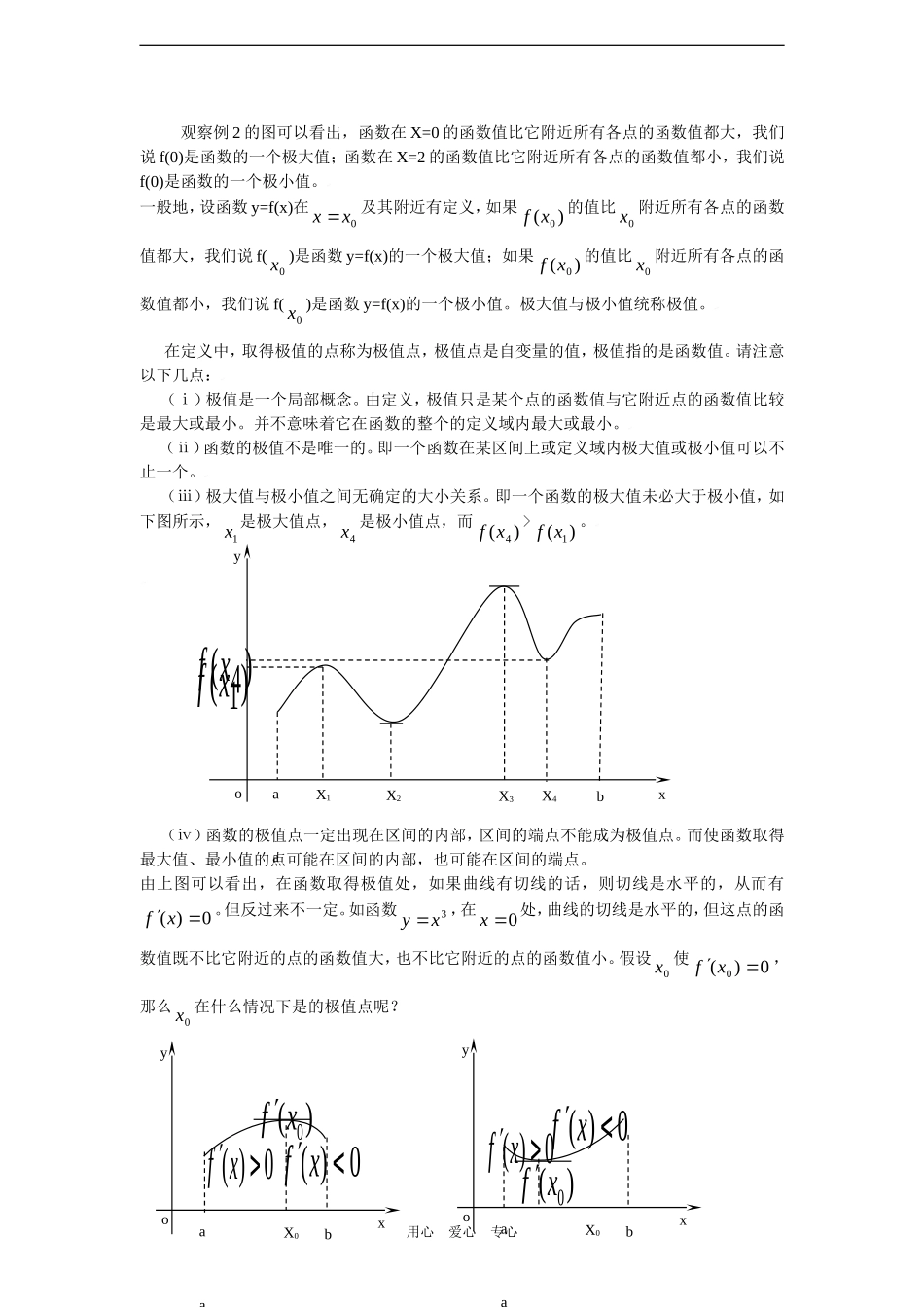
函数的单调性与极值教学目标:正确理解利用导数判断函数的单调性的原理;掌握利用导数判断函数单调性的方法;教学重点:利用导数判断函数单调性;教学难点:利用导数判断函数单调性教学过程:一引入:以前,我们用定义来判断函数的单调性.在假设x10时,函数y=f(x)在区间(2,)内为增函数;在区间(,2)内,切线的斜率为负,函数y=f(x)的值随着x的增大而减小,即/y0时,函数y=f(x)在区间(,2)内为减函数.定义:一般地,设函数y=f(x)在某个区间内有导数,如果在这个区间内/y>0,那么函数y=f(x)在为这个区间内的增函数;,如果在这个区间内/y<0,那么函数y=f(x)在为这个区间内的减函数。例1确定函数422xxy在哪个区间内是增函数,哪个区间内是减函数。例2确定函数76223xxy的单调区间。2极大值与极小值用心爱心专心x02y)(4xf)(1xfoaX1X2X3X4baxyoaX0baxy)(0xf0)(xf0)(xfoaX0baxy)(0xf0)(xf0)(xf观察例2的图可以看出,函数在X=0的函数值比它附近所有各点的函数值都大,我们说f(0)是函数的一个极大值;函数在X=2的函数值比它附近所有各点的函数值都小,我们说f(0)是函数的一个极小值。一般地,设函数y=f(x)在0xx及其附近有定义,如果)(0xf的值比0x附近所有各点的函数值都大,我们说f(0x)是函数y=f(x)的一个极大值;如果)(0xf的值比0x附近所有各点的函数值都小,我们说f(0x)是函数y=f(x)的一个极小值。极大值与极小值统称极值。在定义中,取得极值的点称为极值点,极值点是自变量的值,极值指的是函数值。请注意以下几点:(ⅰ)极值是一个局部概念。由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小。并不意味着它在函数的整个的定义域内最大或最小。(ⅱ)函数的极值不是唯一的。即一个函数在某区间上或定义域内极大值或极小值可以不止一个。(ⅲ)极大值与极小值之间无确定的大小关系。即一个函数的极大值未必大于极小值,如下图所示,1x是极大值点,4x是极小值点,而)(4xf>)(1xf。(ⅳ)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点。而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点。由上图可以看出,在函数取得极值处,如果曲线有切线的话,则切线是水平的,从而有0)(xf。但反过来不一定。如函数3xy,在0x处,曲线的切线是水平的,但这点的函数值既不比它附近的点的函数值大,也不比它附近的点的函数值小。假设0x使0)(0xf,那么0x在什么情况下是的极值点呢?用心爱心专心xoy如上左图所示,若0x是)(xf的极大值点,则0x两侧附近点的函数值必须小于)(0xf。因此,0x的左侧附近)(xf只能是增函数,即0)(xf。0x的右侧附近)(xf只能是减函数,即0)(xf,同理,如上右图所示,若0x是极小值点,则在0x的左侧附近)(xf只能是减函数,即0)(xf,在0x的右侧附近)(xf只能是增函数,即0)(xf,从而我们得出结论:若0x满足0)(0xf,且在0x的两侧)(xf的导数异号,则0x是)(xf的极值点,)(0xf是极值,并且如果)(xf在0x两侧满足“左正右负”,则0x是)(xf的极大值点,)(0xf是极大值;如果)(xf在0x两侧满足“左负右正”,则0x是)(xf的极小值点,)(0xf是极小值。例3求函数44313xxy的极值。三小结1求极值常按如下步骤:①确定函数的定义域;②求导数;③求方程/y=0的根,这些根也称为可能极值点;④检查在方程的根的左右两侧的符号,确定极值点。(最好通过列表法)四巩固练习1确定下列函数的单调区间:(1)7522xxy(2)33xxy2求下列函数的极值用心爱心专心(1)672xxy(2)xxy522(3)xxy273(4)323xxy五课堂作业1确定下列函数的单调区间:(1)24xy(2)2)1(xy(3)522xxy(4)xxxy232求下列函数的极值(1)1042xxy(2)7422xxy(3)1323xxy(4)3126xxy(5)xxxy63423(6)422xxy用心爱心专心