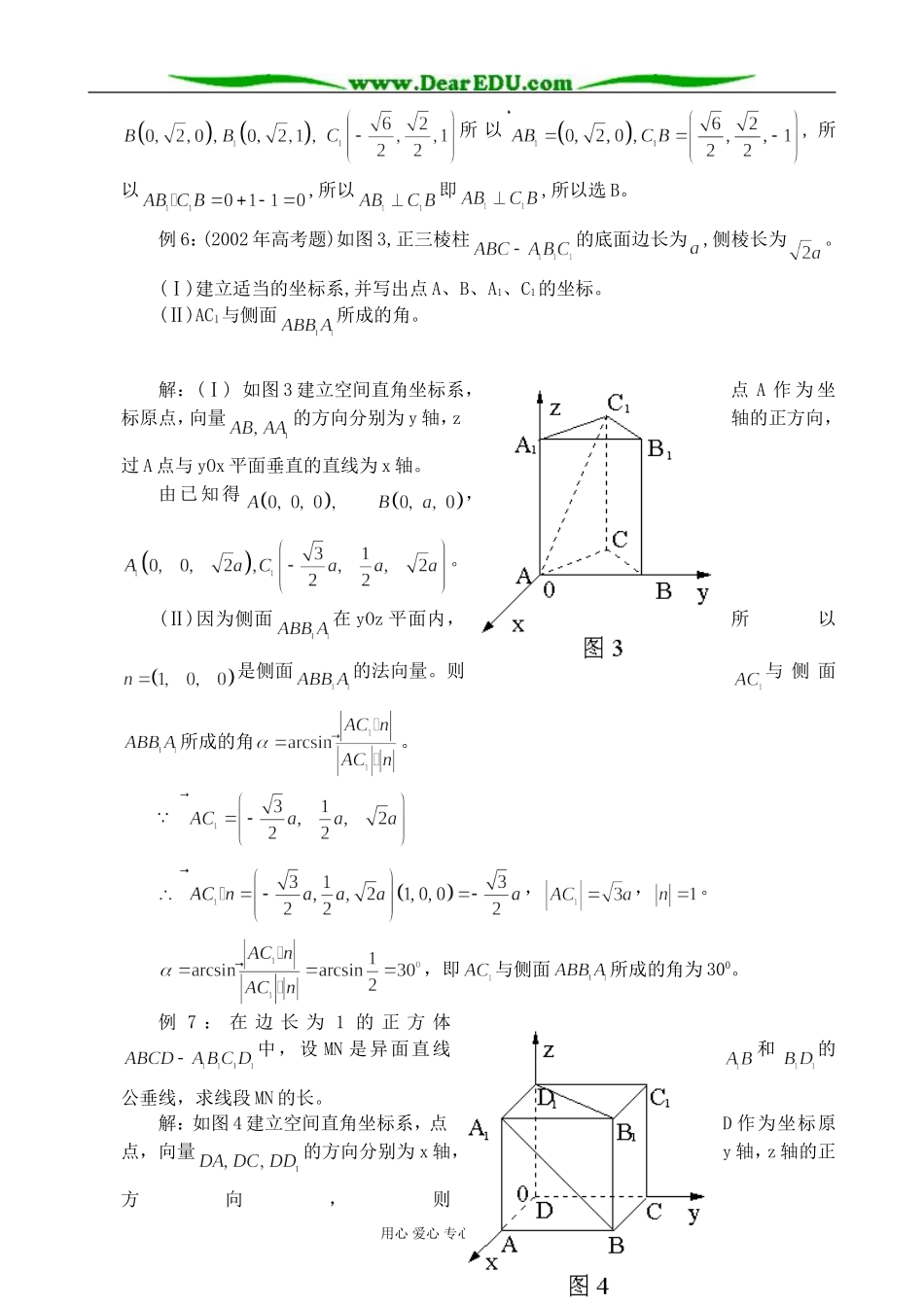
高三数学向量法解题举例利用向量法解题在近几年的高考试题中已多次出现,向量法解题将成为使用试验新教材地区高考命题的一个新的热点,同时向量法解题也是高中几何改革的根本出路。高中数学课程标准中也提出:“应当综合法和向量法并重,以向量法为主”。下面就对向量法解题作一些探讨。一、平面向量例1:(2002年高考题)平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(-1,3),若点C满足,其中,且,则点C的轨迹方程为()(A)(B)(C)(D)分析:这是一道向量的数量积和二次曲线相结合的题,可根据两个向量相等的充要条件列方程组,然后消去就可求出点C的轨迹方程。解:因为。设则消去得点C的轨迹方程是:,所以选D。例2:若抛物线上的点P到直线的距离为最短,则点P的坐标为__________。解:对求导得:,由导数的几何意义知,抛物线上任一点的切线的斜率,则切线的方向向量,而直线的方向向量,根据题意知只有当抛物线上的点满足,即时,求得点到直线的距离最短,所以应填。例3:(2001年高考题)设抛物线的焦点为F,经过点F的直线交抛物线于A,B两点,点C在抛物线上,且轴,证明直线AC经过原点O。分析:要证明直线AC经过原点O,只要证明向量与共线即可。用心爱心专心116号编辑解:如图1:因为抛物线的焦点为。所以经过点F的直线方程可设为,代入抛物线的方程得:。设,则。因为轴,且点C在准线上,所以点C的坐标为。所以。所以,故AC经过原点O。例题4:已知直线与圆交于两点P,Q。求c的值,使(O为坐标原点)。分析:由可得,从而可求出c的值。解:设两交点P,Q的坐标为;把代入得。所以。所以。因为;所以,即,解这个方程得。二、空间向量例5:(2001年高考题)在正三棱柱中,若,则与所成角的大小为()(A)(B)(C)(D)解:如图2建立空间直角坐系,点A作为坐标原点,向量的方向分别为y轴,z轴的正方向,过A点与yOz平面垂直的直线为x轴。设BB1=1,则AB=,用心爱心专心116号编辑所以,所以,所以即,所以选B。例6:(2002年高考题)如图3,正三棱柱的底面边长为,侧棱长为。(Ⅰ)建立适当的坐标系,并写出点A、B、A1、C1的坐标。(Ⅱ)AC1与侧面所成的角。解:(Ⅰ)如图3建立空间直角坐标系,点A作为坐标原点,向量的方向分别为y轴,z轴的正方向,过A点与yOx平面垂直的直线为x轴。由已知得,。(Ⅱ)因为侧面在yOz平面内,所以是侧面的法向量。则与侧面所成的角。,,。,即与侧面所成的角为300。例7:在边长为1的正方体中,设MN是异面直线和的公垂线,求线段MN的长。解:如图4建立空间直角坐标系,点D作为坐标原点,向量的方向分别为x轴,y轴,z轴的正方向,则用心爱心专心116号编辑,,所以又设是异面直线和的公垂线的一个方向向量,则,解这个方程组得即线段MN的长是。例8:如图5,在底面是直角梯形的四棱锥中,,SA底面ABCD,SA=AB=BC=1,AD=。(Ⅰ)求点A到平面SDC的距离。(Ⅱ)求平面SCD与平面SBA所成二面角的大小。解:(Ⅰ)如图5,建立空间直角坐标系,点A为坐标原点,向量,的方向分别为x轴,y轴,z轴的正方向,则,。。又设平面SCD的法向量为解这个方程组得。用心爱心专心116号编辑。(Ⅱ)因为是平面SBA的法向量,n是平面SCD的法向量,所以平面SCD与平面SBA所成二面角的大小为。注:相关结论结论1:如图6,设是两条异面直线,n是公垂线段AB的方向向量,又C、D分别是上的任意两点,则①的夹角为;②。结论2:如图7,设n是平面的法向量,AB是平面的一条斜线,其中,则①AB与平面所成的角为;②点B到平面的距离为。结论3:如图8,设分别是二面角的面的法向量;则就是所求二面角的平面角或其补角的大小。结论4:如图9,AB、CD分别是二面角的两个面内与棱l垂直的异面直线,则二面角的大小为。用心爱心专心116号编辑郭宾生2003年4月用心爱心专心116号编辑