名思教育个性化辅导教案--探究VIP免费

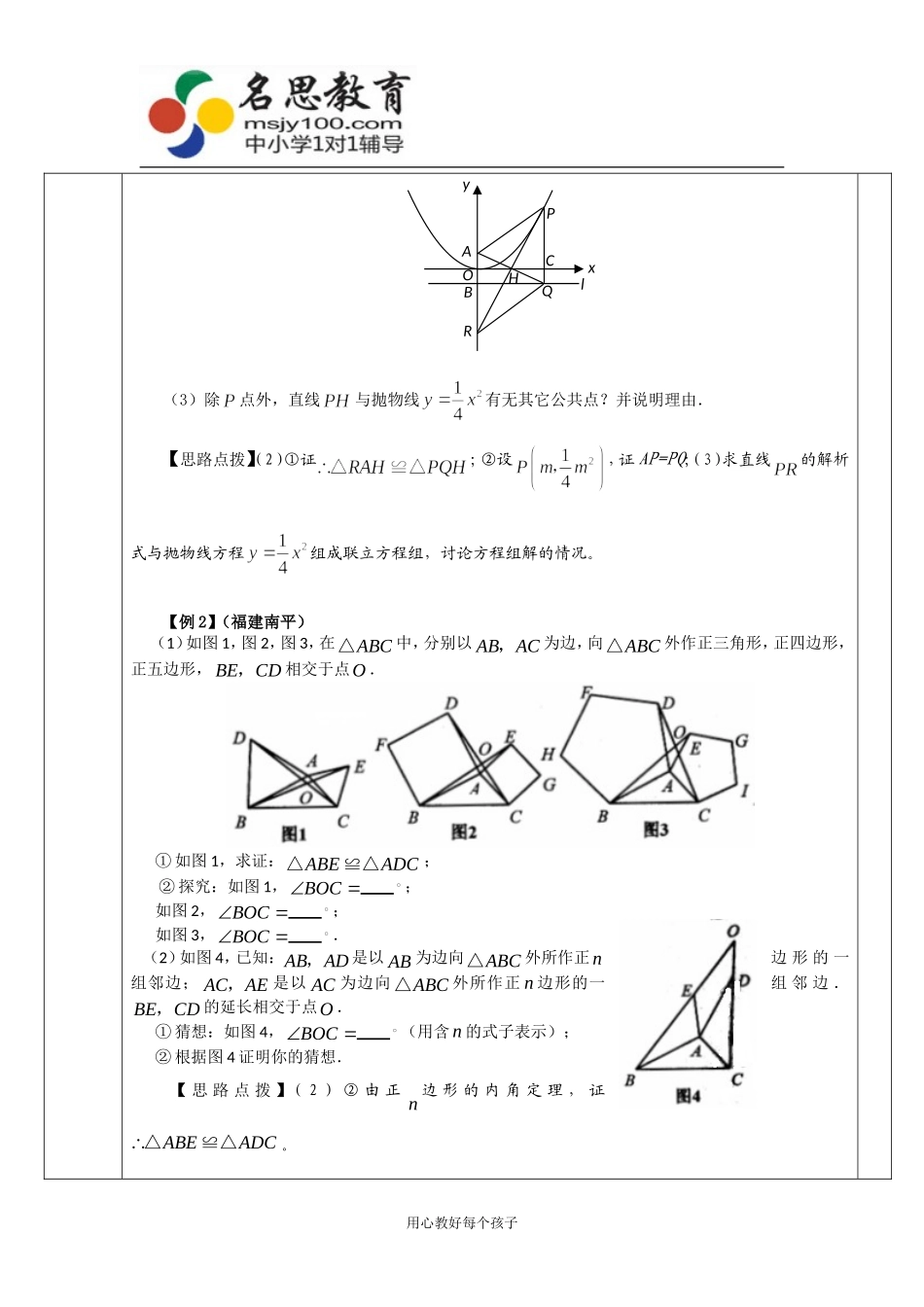
名思教育个性化辅导教案学科：授课老师：授课时间：年月日时分——时分学生姓名年级课时课题及教学内容教学目标教学重、难点环节教师授课过程反思主要知识中考数学专题讲座探究、操作性问题【知识纵横】探索研究是通过对题意的理解，解题过程由简单到难，在承上启下的作用下，引导学生思考新的问题，大胆进行分析、推理和归纳，即从特殊到一般去探究，以特殊去探求一般从而获得结论，有时还要用已学的知识加以论证探求所得结论。操作性问题是让学生按题目要求进行操作，考察学生的动手能力、想象能力和概括能力。【典型例题】【例1】（江苏镇江)探索研究如图，在直角坐标系中，点为函数在第一象限内的图象上的任一点，点的坐标为，直线过且与轴平行，过作轴的平行线分别交轴，于，连结交轴于，直线交轴于．（1）求证：点为线段的中点；（2）求证：①四边形为平行四边形；②平行四边形为菱形；用心教好每个孩子（3）除点外，直线与抛物线有无其它公共点？并说明理由．【思路点拨】（2）①证；②设，证AP=PQ;（3）求直线的解析式与抛物线方程组成联立方程组，讨论方程组解的情况。【例2】（福建南平）（1）如图1，图2，图3，在ABC△中，分别以ABAC，为边，向ABC△外作正三角形，正四边形，正五边形，BECD，相交于点O．①如图1，求证：ABEADC△≌△；②探究：如图1，BOC；如图2，BOC；如图3，BOC．（2）如图4，已知：ABAD，是以AB为边向ABC△外所作正n边形的一组邻边；ACAE，是以AC为边向ABC△外所作正n边形的一组邻边．BECD，的延长相交于点O．①猜想：如图4，BOC（用含n的式子表示）；②根据图4证明你的猜想．【思路点拨】（2）②由正n边形的内角定理，证ABEADC△≌△。用心教好每个孩子xlQCPAOBHRy【例3】（内江市）在一平直河岸l同侧有AB，两个村庄，AB，到l的距离分别是3km和2km，kmABa(1)a．现计划在河岸l上建一抽水站P，用输水管向两个村庄供水．方案设计某班数学兴趣小组设计了两种铺设管道方案：图13-1是方案一的示意图，设该方案中管道长度为1d，且1(km)dPBBA（其中BPl于点P）；图13-2是方案二的示意图，设该方案中管道长度为2d，且2(km)dPAPB（其中点A与点A关于l对称，AB与l交于点P）．观察计算（1）在方案一中，1dkm（用含a的式子表示）；（2）在方案二中，组长小宇为了计算2d的长，作了如图13-3所示的辅助线，请你按小宇同学的思路计算，2dkm（用含a的式子表示）．探索归纳（1）①当4a时，比较大小：12_______dd（填“＞”、“＝”或“＜”）；②当6a时，比较大小：12_______dd（填“＞”、“＝”或“＜”）；（2）请你参考右边方框中的方法指导，就a（当1a时）的所有取值情况进行分析，要使铺设的管道长度较短，应选择方案一还是方案二？【思路点拨】参考方法指导解答探索归纳（2）。用心教好每个孩子ABPllABPAC图13-1图13-2lABPAC图13-3K方法指导当不易直接比较两个正数与的大小时，可以对它们的平方进行比较：，，与的符号相同．当时，，即；当时，，即；当时，，即；【例4】（浙江宁波）如图1，把一张标准纸一次又一次对开，得到“2开”纸、“4开”纸、“8开”纸、“16开”纸…．已知标准纸的短边长为．（1）如图2，把这张标准纸对开得到的“16开”张纸按如下步骤折叠：第一步将矩形的短边与长边对齐折叠，点落在上的点处，铺平后得折痕；第二步将长边与折痕对齐折叠，点正好与点重合，铺平后得折痕．则的值是，的长分别是，．（2）“2开”纸、“4开”纸、“8开”纸的长与宽之比是否都相等？若相等，直接写出这个比值；若不相等，请分别计算它们的比值．（3）如图3，由8个大小相等的小正方形构成“”型图案，它的四个顶点分别在“16开”纸的边上，求的长．（4）已知梯形中，，，，且四个顶点都在“4开”纸的边上，请直接写出2个符合条件且大小不同的直角梯形的面积．【思路点拨】（3）证,，设，建立关于x的方程解之；（4）参考图3分二类情形讨论。【学力训练】1、（山东聊城）探索研究：如图，把一张长10cm，宽8cm的矩形硬纸板的四周各剪去一个同样大小的正方形，再折合成一个无盖的长方体盒子（纸板的厚...