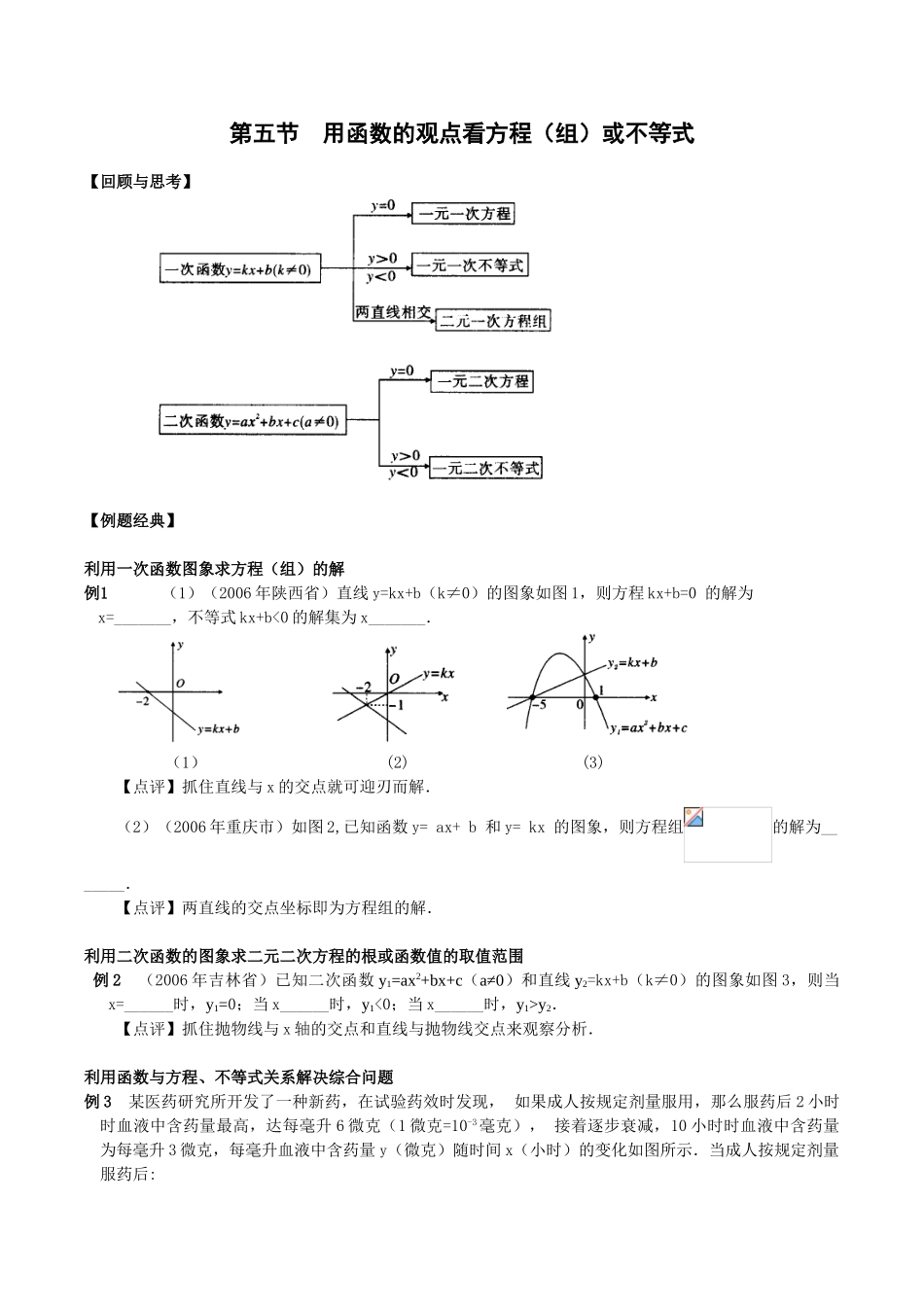
第五节用函数的观点看方程(组)或不等式【回顾与思考】【例题经典】利用一次函数图象求方程(组)的解例1(1)(2006年陕西省)直线y=kx+b(k≠0)的图象如图1,则方程kx+b=0的解为x=_______,不等式kx+b<0的解集为x_______.(1)(2)(3)【点评】抓住直线与x的交点就可迎刃而解.(2)(2006年重庆市)如图2,已知函数y=ax+b和y=kx的图象,则方程组的解为_______.【点评】两直线的交点坐标即为方程组的解.利用二次函数的图象求二元二次方程的根或函数值的取值范围例2(2006年吉林省)已知二次函数y1=ax2+bx+c(a≠0)和直线y2=kx+b(k≠0)的图象如图3,则当x=______时,y1=0;当x______时,y1<0;当x______时,y1>y2.【点评】抓住抛物线与x轴的交点和直线与抛物线交点来观察分析.利用函数与方程、不等式关系解决综合问题例3某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示.当成人按规定剂量服药后:(1)分别求出x≤2和x≥2时x与y之间的函数关系式;(2)如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长?【点评】从图中提供有效信息建立函数关系,并转化为不等式为解决.【考点精练】基础训练1.(2006年广西省)已知y=-2x+m,当x=3时,y=1,则直线y=-2x+m与x轴的交点坐标为_______.2.若直线y=x-2与直线y=-x+a相交于x轴,则直线y=-x+a不经过的象限是_____.3.若不等式kx+b>0的解集为x>-2,则直线y=kx+b与x轴的交点为_____.4.(2006年衡阳市)如图,直线y1=k1x+b1与直线y2=k2x+b2交于点(-2,2),则当x____时,y10的解集为()A.x>0B.x<0C.x<2D.x>28.(2006年安徽省)已知甲、乙两弹簧的长度y(cm)与所挂物体质量x(kg)之间的函数解析式分别为y1=k1x+a1和y2=k2x+a2,图象如图所示,设所挂物体质量为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为()A.y1>y2B.y1=y2C.y1