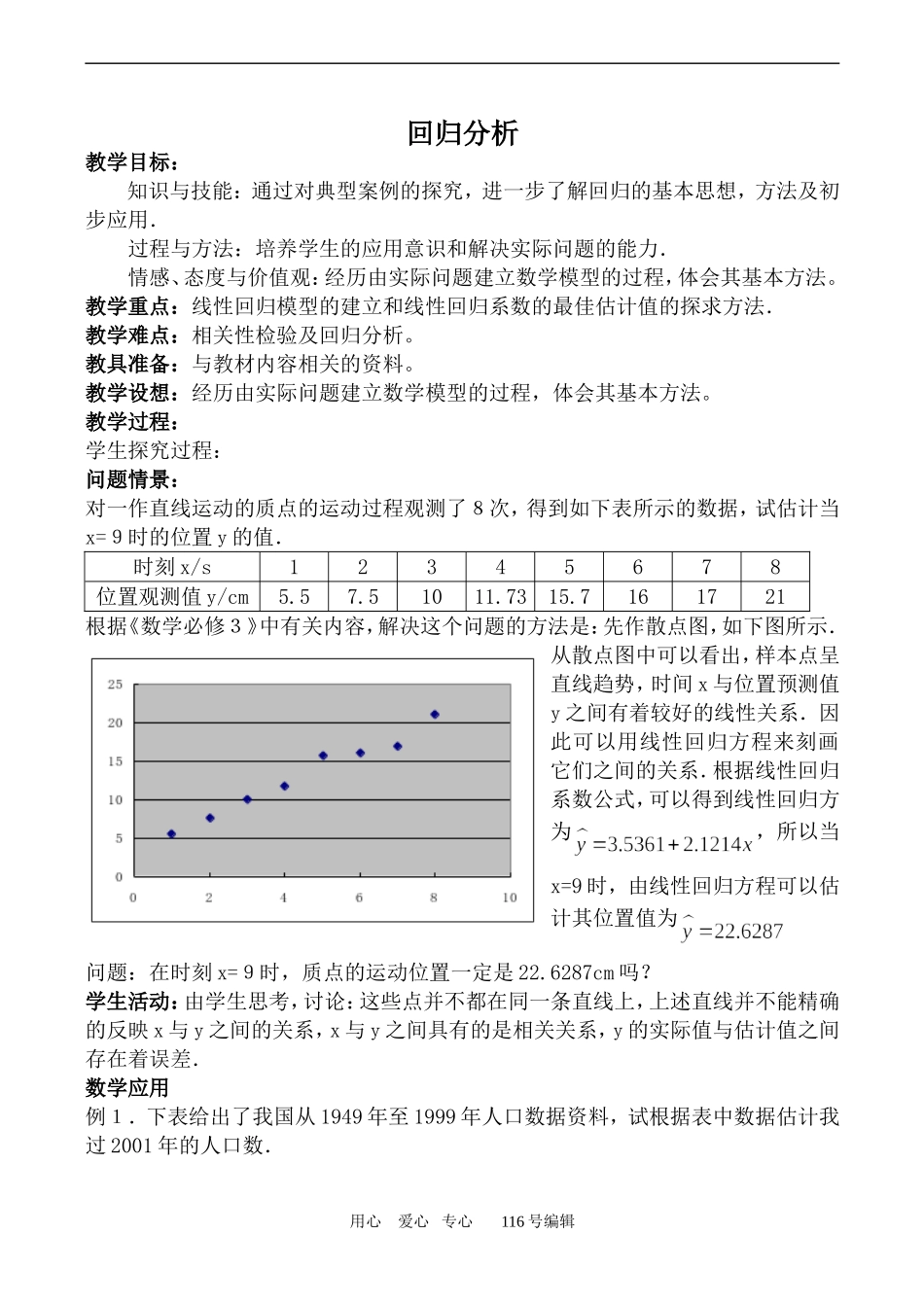
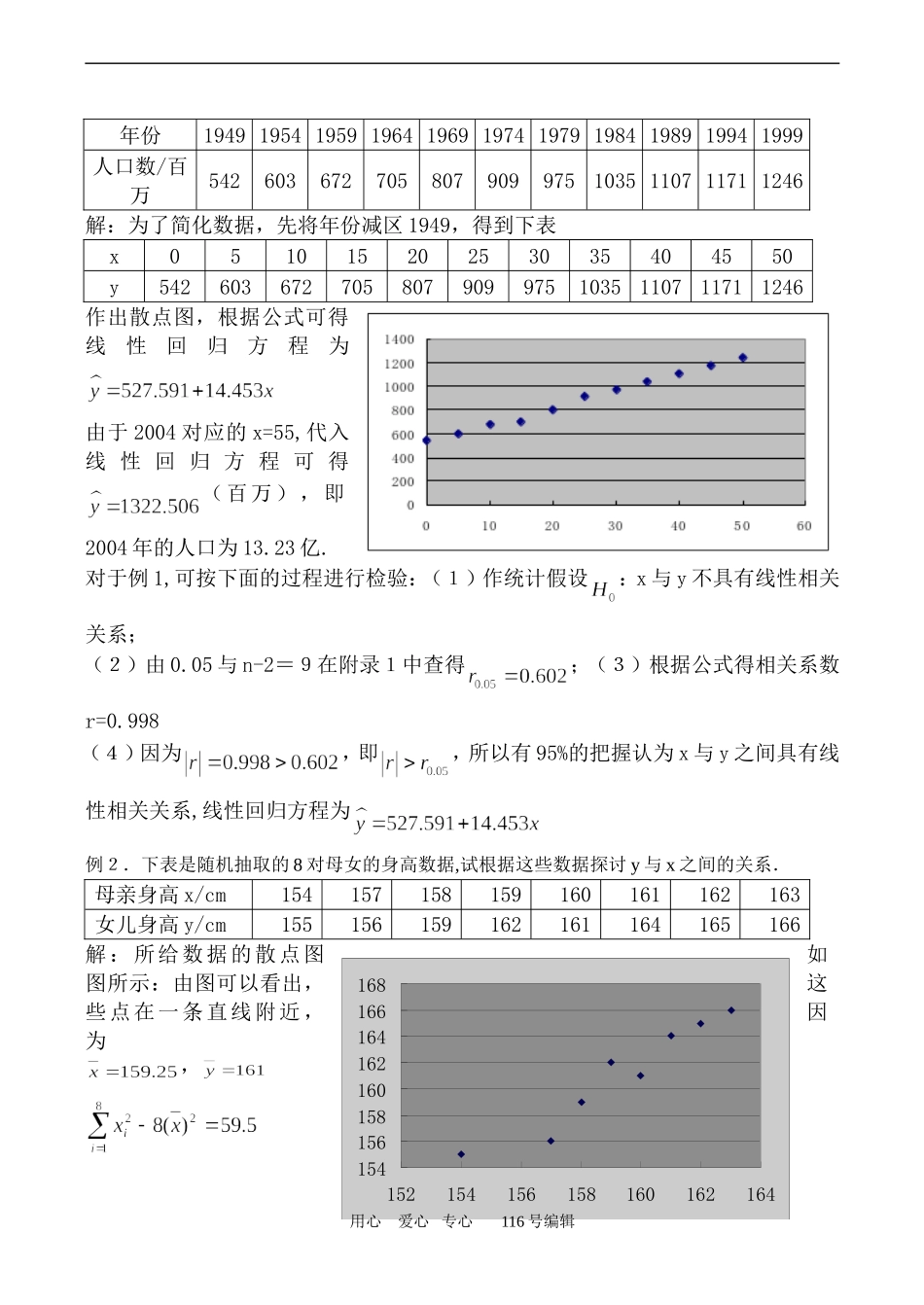
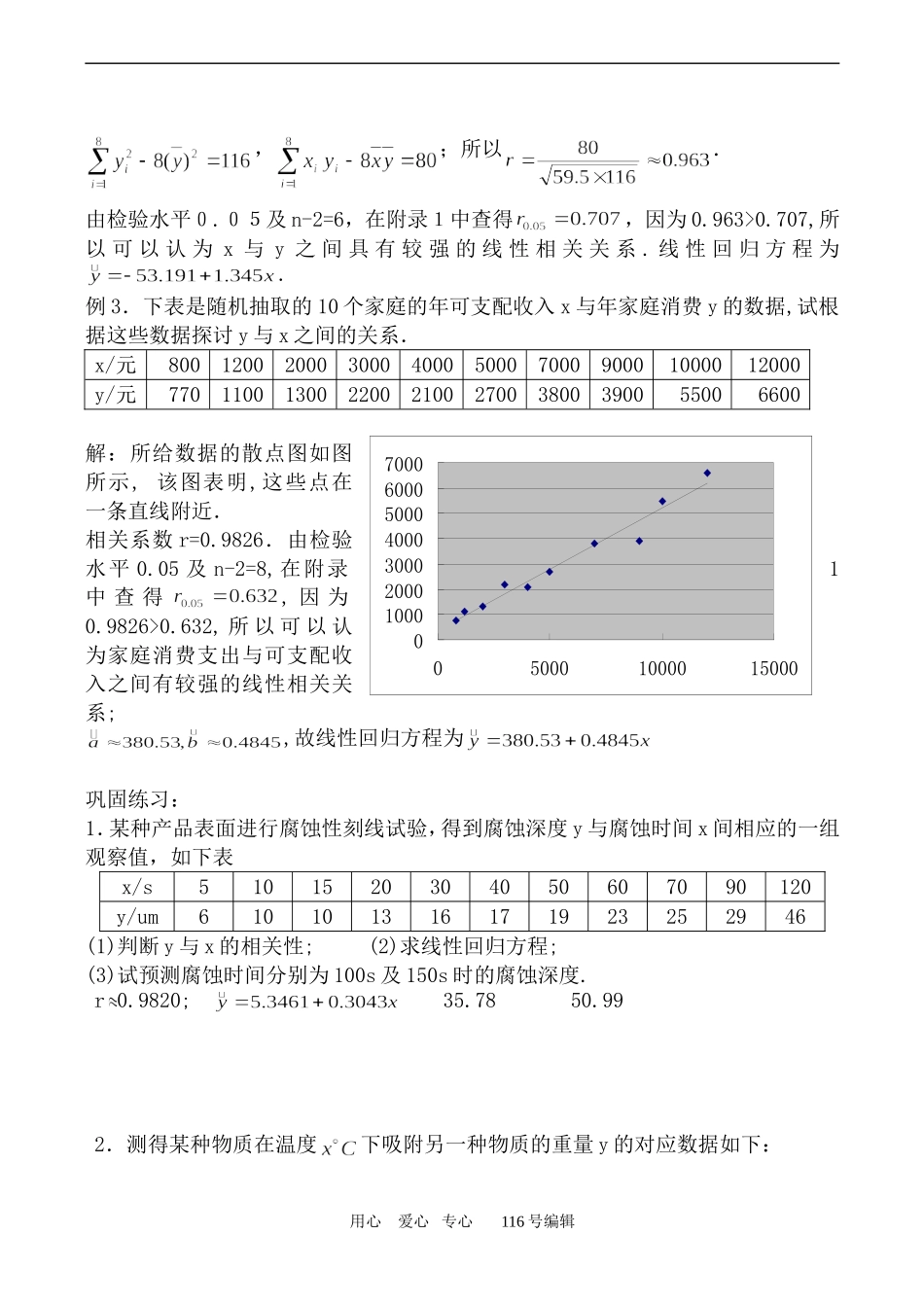
回归分析教学目标:知识与技能:通过对典型案例的探究,进一步了解回归的基本思想,方法及初步应用.过程与方法:培养学生的应用意识和解决实际问题的能力.情感、态度与价值观:经历由实际问题建立数学模型的过程,体会其基本方法。教学重点:线性回归模型的建立和线性回归系数的最佳估计值的探求方法.教学难点:相关性检验及回归分析。教具准备:与教材内容相关的资料。教学设想:经历由实际问题建立数学模型的过程,体会其基本方法。教学过程:学生探究过程:问题情景:对一作直线运动的质点的运动过程观测了8次,得到如下表所示的数据,试估计当x=9时的位置y的值.时刻x/s12345678位置观测值y/cm5.57.51011.7315.7161721根据《数学必修3》中有关内容,解决这个问题的方法是:先作散点图,如下图所示.从散点图中可以看出,样本点呈直线趋势,时间x与位置预测值y之间有着较好的线性关系.因此可以用线性回归方程来刻画它们之间的关系.根据线性回归系数公式,可以得到线性回归方为,所以当x=9时,由线性回归方程可以估计其位置值为问题:在时刻x=9时,质点的运动位置一定是22.6287cm吗?学生活动:由学生思考,讨论:这些点并不都在同一条直线上,上述直线并不能精确的反映x与y之间的关系,x与y之间具有的是相关关系,y的实际值与估计值之间存在着误差.数学应用例1.下表给出了我国从1949年至1999年人口数据资料,试根据表中数据估计我过2001年的人口数.用心爱心专心116号编辑154156158160162164166168152154156158160162164年份19491954195919641969197419791984198919941999人口数/百万5426036727058079099751035110711711246解:为了简化数据,先将年份减区1949,得到下表x05101520253035404550y5426036727058079099751035110711711246作出散点图,根据公式可得线性回归方程为由于2004对应的x=55,代入线性回归方程可得(百万),即2004年的人口为13.23亿.对于例1,可按下面的过程进行检验:(1)作统计假设:x与y不具有线性相关关系;(2)由0.05与n-2=9在附录1中查得;(3)根据公式得相关系数r=0.998(4)因为,即,所以有95%的把握认为x与y之间具有线性相关关系,线性回归方程为例2.下表是随机抽取的8对母女的身高数据,试根据这些数据探讨y与x之间的关系.母亲身高x/cm154157158159160161162163女儿身高y/cm155156159162161164165166解:所给数据的散点图如图所示:由图可以看出,这些点在一条直线附近,因为,用心爱心专心116号编辑01000200030004000500060007000050001000015000,;所以.由检验水平0.05及n-2=6,在附录1中查得,因为0.963>0.707,所以可以认为x与y之间具有较强的线性相关关系.线性回归方程为.例3.下表是随机抽取的10个家庭的年可支配收入x与年家庭消费y的数据,试根据这些数据探讨y与x之间的关系.x/元80012002000300040005000700090001000012000y/元770110013002200210027003800390055006600解:所给数据的散点图如图所示,该图表明,这些点在一条直线附近.相关系数r=0.9826.由检验水平0.05及n-2=8,在附录1中查得,因为0.9826>0.632,所以可以认为家庭消费支出与可支配收入之间有较强的线性相关关系;,故线性回归方程为巩固练习:1.某种产品表面进行腐蚀性刻线试验,得到腐蚀深度y与腐蚀时间x间相应的一组观察值,如下表x/s5101520304050607090120y/um610101316171923252946(1)判断y与x的相关性;(2)求线性回归方程;(3)试预测腐蚀时间分别为100s及150s时的腐蚀深度.r0.9820;35.7850.992.测得某种物质在温度下吸附另一种物质的重量y的对应数据如下:用心爱心专心116号编辑x1.51.82.433.54.44.83.95.0y4.85.77.08.310.913.113.612.415.3(1)对变量y与x进行相关性检验;(2)求线性回归方程r0.9913.在某个文艺网络中,点击观看某节目的累计人次和播放天数如下表:播放天数12345678910累计人数51134213235262294330378457533(1)画出散点图;(2)判断是否有线性相关关系,求回归直线方程是否有意义;(3)求回归直线方程;(4)当播放天数为11天时,估计累计人次为多少?r0.984547人教学反思:建构数学:1.线性回归模型:我们将称...