柱体、锥体与台体的体积·评价练习VIP免费

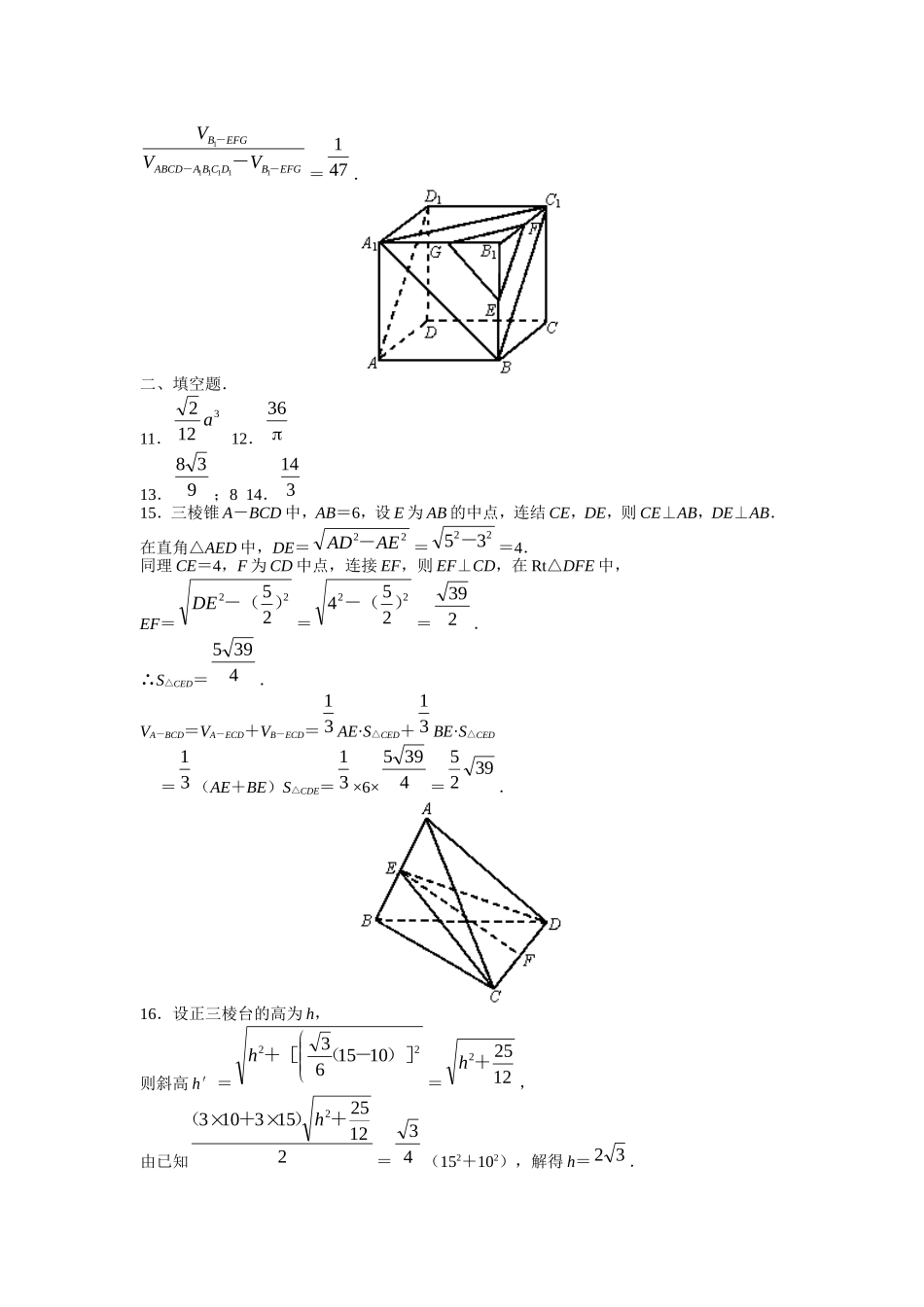
柱体、锥体与台体的体积·评价练习一、选择题1．若正方体的全面积增为原来的2倍，那么它的体积增为原来的（）A．2倍B．4倍C．2倍D．22倍2．一个长、宽、高分别为a、b、c长方体的体积是8cm2，它的全面积是32cm2，且满足b2＝ac，那么这个长方体棱长的和是（）A、28cmB．32cmC．36cmD．40cm3．正六棱台的两底面的边长分别为a和2a，高为a，则它的体积为（）A．32321aB．3233aC．337aD．3237a4．若球的体积与其表面积的数值相等，则球的半径为（）A．1B．3C．2D．215．一个球的外切正方体的全面积的数值等于6cm2，则此球的体积为（）A．334cmB．386cmC．361cmD．366cm6．正六棱锥的底面边长为a，体积为323a，那么侧棱与底面所成的角为（）A．6B．4C．3D．1257．正四棱锥的底面面积为Q，侧面积为S，则它的体积为（）A、SQ31B．)(2122QSQC、)(2122QSSD、)(6122QSQ8．棱台上、下底面面积之比为1∶9，则棱台的中截面分棱台成两部分的体积之比是（）A．1∶7B．2∶7C．7∶19D．3∶169．正方体、等边圆柱与球它们的体积相等，它们的表面积分别为S1、S2、S3，下面关系中成立的是（）A．S3＞S2＞S1B．S1＞S3＞S2C．S1＞S2＞S3D．S2＞Sl＞S310．沿棱长为1的正方体的交于一点的三条棱的中点作一个截面，截得一个三棱锥，那么截得的三棱锥的体积与剩下部分的体积之比是（）A．1∶5B．1∶23C．1∶11D．1∶47二、填空题11．底面边长和侧棱长都是a的正三棱锥的体积是_______．12．将4×6的矩形铁皮作为圆柱的侧面卷成一个圆柱，则圆柱的最大体积是_______．13．半径为1的球的内接正方体的体积是________；外切正方体的体积是_______．14．已知正三棱台上、下底面边长分别为2、4，且侧棱与底面所成角是45°，那么这个正三棱台的体积等于_______．三、解答题15．三棱锥的五条棱长都是5，另一条棱长是6，求它的体积．16．两底面边长分别是15cm和10cm的正三棱台，它的侧面积等于两底面积的和，求它的体积．17．一个圆锥形容器和一个圆柱形容器，它们的轴截面尺寸如图所示，两容器内所盛液体的体积正好相等，且液面高度h正好相同，求h．18．如图所示，已知正方体ABCD—A1B1ClDl的棱长为a，E为棱AD的中点，求点A1到平面BED1的距离．参考答案一、选择题1．D2．B解：由已知③＝②＝＋＋①＝acbcabcabcba2168··③代入①得b3＝8，b＝2，ac＝4，代入②a＋c＝6．∴长方体棱长的和为4（a＋b＋c）＝4×8＝32（cm2）．3．D4．B5．C6．B7．D设正四棱锥的底面边长和高分别为a，h，斜高为h′，则h′＝222）＋（ah，S＝21（4a）h′＝2a224ah＋解得h＝22244aaS－＝442QQS－＝QQS2221－．V＝31h·Q＝31（QQS2221－）Q＝）－（2261QSQ．8．C9．B10．D由E、F、G分别为BB1，B1C1，B1A1的中点，可证明平面EFG∥平面BC1A1，因此1111ABCBEFGBVV－－＝31）（BCEF＝（21）3＝81．即EFGBV－1＝81111ABCBV－＝81·31ADABCBV111－＝81（31·211111DCBAABCDV－）＝4811111DCBAABCDV－，EFGBDCBAABCDEFGBVVV－－－－111111＝471．二、填空题．11．3122a12．3613．938；814．31415．三棱锥A－BCD中，AB＝6，设E为AB的中点，连结CE，DE，则CE⊥AB，DE⊥AB．在直角△AED中，DE＝22AEAD－＝2235－＝4．同理CE＝4，F为CD中点，连接EF，则EF⊥CD，在Rt△DFE中，EF＝2225）－（DE＝22254）－（＝239．∴S△CED＝4395．VA－BCD＝VA－ECD＋VB－ECD＝31AE·S△CED＋31BE·S△CED＝31（AE＋BE）S△CDE＝31×6×4395＝3925．16．设正三棱台的高为h，则斜高h′＝22101563）］－（＋［h＝12252＋h，由已知212251531032＋）＋（h＝43（152＋102），解得h＝32．因此V＝31·32（43·102＋43·152＋2215·1043）＝2475（cm3）．别解：设上、下底面面积分别是S1，S2（S1＜S2），侧面与底面成二面角为α，由已知，S侧＝S1＋S2①．又S侧cosα＝S2－S1②，②÷①，cosα＝2112SSSS＋－＝22221043154310431543＋－＝135．然后再求棱台的高和体积．17．设圆锥形容器的液面的半径为R，则液体的体积为31πR2h，圆柱形容器内的液体体积为π（2a）2h．根据题意，有31πR2h＝π（2a）2h，解得R＝a23．再根据圆锥轴截面与内盛液体轴截面是相似三角形，得aa23＝ah，所以h＝a23．18．解：EDAS11＝21A1D1·AA1＝22a．D1B＝3a，D1E＝BE＝22ABAE＋＝2221aa＋）（＝a25．等腰△EBD1的高为2122）－（BDBE＝222325）－（）（aa＝a22．1BEDS＝21（a3）（a22）＝246a．设A1到平面BED1的距离为h，而11BEDAV－＝EDABV11－，即131BEDS·h＝EDAS1131·AB．∴31·246a·h＝31·22a·a，解得h＝a631．