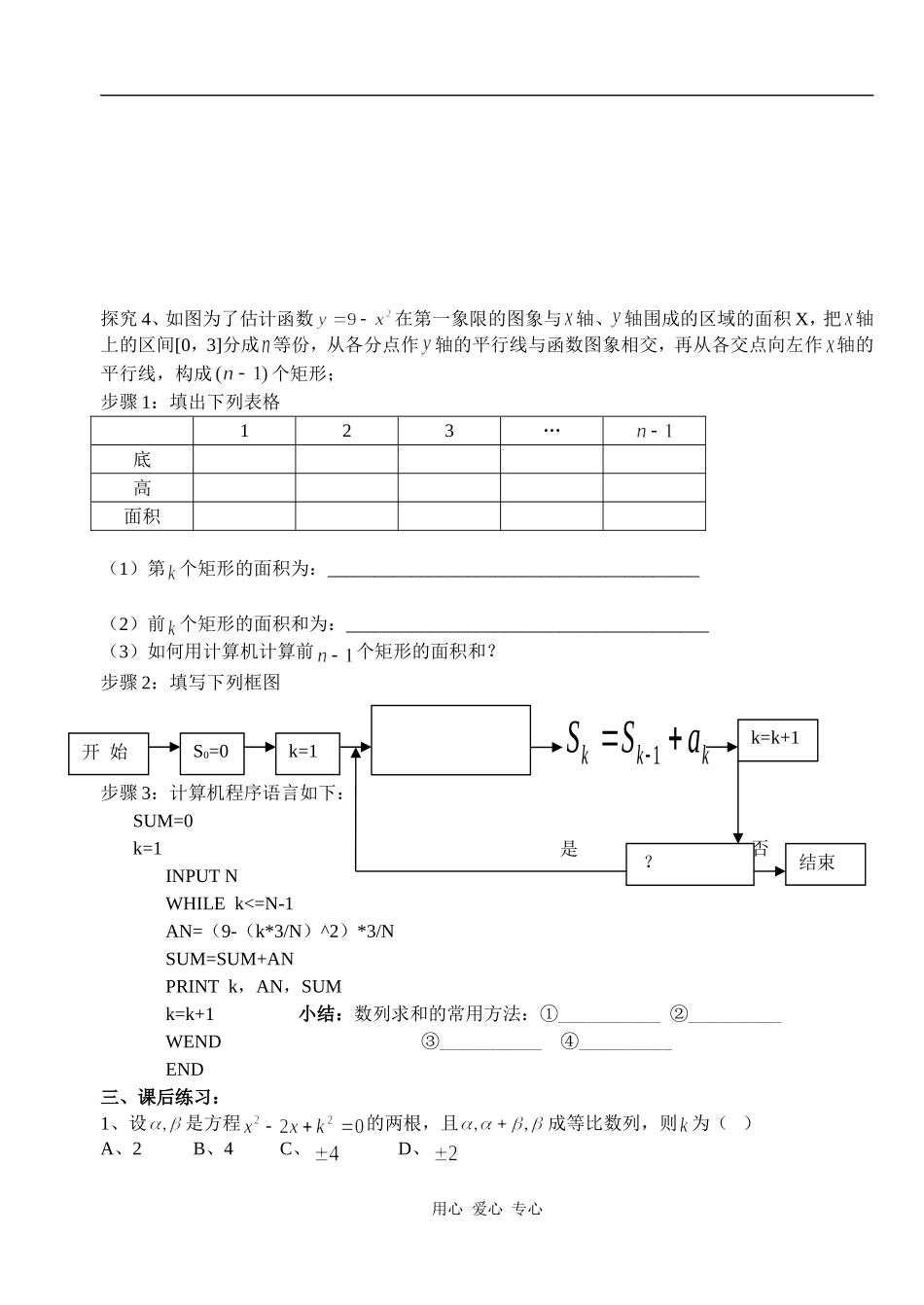
等比数列前n项和(第2课时共2课时)班级________________姓名________________学号__________________目标:1、应用等差、等比数列求和公式进行求和;2、信息技术在数列求和中的应用;重点:应用等差、等比数列求和公式进行求和;难点:错位相减法在求和中的应用;教学过程设计一、温故知新1、填写下列表格:等差数列等比数列定义式通项公式中项公式性质1性质2前n项和公式2、课堂练习:(1)=_____________________(2)_______________________________二、新课探究:探究1、求和:;探究2、求和:;探究3、求和;用心爱心专心探究4、如图为了估计函数在第一象限的图象与轴、轴围成的区域的面积X,把轴上的区间[0,3]分成等份,从各分点作轴的平行线与函数图象相交,再从各交点向左作轴的平行线,构成个矩形;步骤1:填出下列表格123…底高面积(1)第个矩形的面积为:________________________________________(2)前个矩形的面积和为:_______________________________________(3)如何用计算机计算前个矩形的面积和?步骤2:填写下列框图步骤3:计算机程序语言如下:SUM=0k=1INPUTNWHILEk<=N-1AN=(9-(k*3/N)^2)*3/NSUM=SUM+ANPRINTk,AN,SUMk=k+1小结:数列求和的常用方法:①___________②__________WEND③___________④__________END三、课后练习:1、设是方程的两根,且成等比数列,则为()A、2B、4C、D、用心爱心专心是否结束开始S0=0k=1k=k+1kkkaSS1?2、等比数列中,前n项和,则等于()A、-1B、0C、1D、33、已知数列的前n项和(是不为0的实数),那么()A、一定是等差数列B、一定是等比数列C、或者是等差数列,或者是等比数列D、既不可能是等差数列,也不可能是等比数列4、数列中,对于所有的都有,则()A、B、C、D、5、下列四个数中,哪个是数列中的一项()A、380B、39C、35D、236、已知等比数列的前项和,则_______3mS7、求和:(1)(2)(3)用心爱心专心8、一个球从100m高处自由落下,每次着地后又跳回到原高度的一半在落下,(1)当它第10次着地时,经过的路程共是多少?(2)当它是第几次着地时,经过的路程共是m?9、某林场2002年底森林木材储存量为330万立方米,若树林以每年25%的增长率生长,计划从2003年起,每年冬天要砍伐的木材量为万立方米,为了实现经过20年木材储存量翻两番的目标,每年砍伐的木材量的最大值是多少?()用心爱心专心