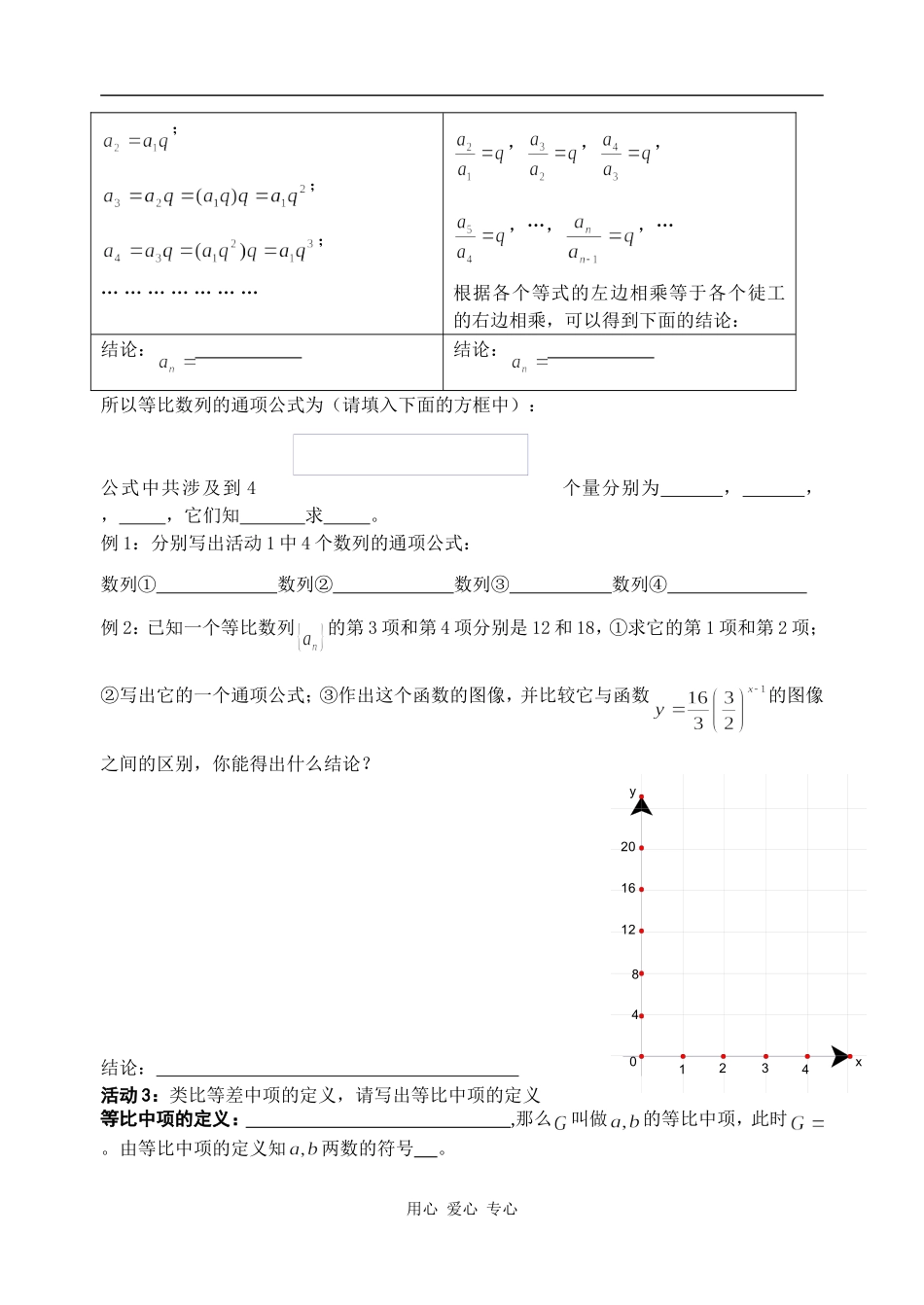
等比数列(第1课时,总2课时)班级姓名学号学习目标1.掌握等比数列的定义;理解等比数列的通项公式及推导;2.能在具体的问题中发现数列的等比关系,体会等比数列与指数函数的关系。学习重点:等比数列的概念及通项公式学习难点:灵活应用定义式及通项公式解决相关问题教学过程设计一、温故知新:1.等差数列的定义:,即,我们把这个常数就叫做等差数列的,用符号来表示。2.等差数列的通项公式为,而()。3.等差中项的概念:。二、新课讲解:活动1:观察下面4个数列,分析它们具有什么的特点?数列①:1,2,4,8,…数列②:1,…数列③:…数列④:,,,,…分析:对于数列①,从第二项起,每一项与前一项的比都等于;对于数列②,从第二项起,每一项与前一项的比都等于;对于数列③,从第二项起,每一项与前一项的比都等于;对于数列④,从第二项起,每一项与前一项的比都等于;结论1:上面4个数列的共同特点是。等比数列的定义:。结论2:根据等比数列的定义知上面4个数列都是,而且它们的公比依次是,,,。活动2:等差数列具有通项公式,给研究等差数列带来了极大的方便,那么等比数列是否同样具有通项公式呢?下面让我们一起来探究等比数列的通项公式。设等比数列的首项为,公比为,根据等比数列的定义可以得到:方法一(不完全归纳法)方法二(叠乘法)用心爱心专心;;;…………………,,,,…,,…根据各个等式的左边相乘等于各个徒工的右边相乘,可以得到下面的结论:结论:结论:所以等比数列的通项公式为(请填入下面的方框中):公式中共涉及到4个量分别为,,,,它们知求。例1:分别写出活动1中4个数列的通项公式:数列①数列②数列③数列④例2:已知一个等比数列的第3项和第4项分别是12和18,①求它的第1项和第2项;②写出它的一个通项公式;③作出这个函数的图像,并比较它与函数的图像之间的区别,你能得出什么结论?结论:活动3:类比等差中项的定义,请写出等比中项的定义等比中项的定义:,那么叫做的等比中项,此时。由等比中项的定义知两数的符号。用心爱心专心160xy1234481220考考你:设三个数成等比数列,其中,那么。例3:某种放射性物质不断变化为其他物质,每经过一年剩留的这物质是原来的84%,这种物质的半衰期为多长(精确到1年)。(参考数据:lg84=1.92,lg2=0.30)三、课内练习:1.已知数列是一个等比数列,在下表中填入适当的数。21620.52.已知一种计算机病毒可以利用电子邮件进行传播。如果第一轮感染的计算机数是80台,并且从第一轮起,以后各轮的每一台计算机都可以感染下一轮的20台计算机。那么到第轮可以感染的计算机台数,到第5轮感染到台的计算机。3.在9与343中间插入两个数,使9,,343成等比数列,则,。四、课外练习:1.设等比数列的前3个数依次为,则()A.1B.C.D.2.设等比数列的首项为98,末项为3,公比为,则这个数列的项数为()A.3B.4C.5D.63.设,,,成等比数列,其公比为2,则=()A.B.C.D.14.若是互异的正数,是的等差中项,是的等比中项,则与的大小关系为()A.B.C.GAD.不能确定5.等差数列na的公差,若成等比数列,则=()用心爱心专心A.B.C.D.16136.一个蜂巢里有1只蜜蜂。第1天,它飞出去找回了5个伙伴;第2天,6只蜜蜂飞出去,各自找回了5个伙伴……如果这个找伙伴的过程继续下去,第6天所有的蜜蜂都归巢后,蜂巢中一共有多少只蜜蜂()A.5986B.6656C.216D.367.在等比数列中,(1)若3,274qa,则;(2)若,则,公比=;(3)若,则,通项公式=。8.在数列na中,已知,且,则数列的通项公式为.若是与的等差中项,则=。9.数列,……的一个通项公式为。10.若160,,5成等比数列,则的值分别为。11.某地为了保持水土资源,实行退耕还林,如果2000年退耕8万公顷,以后每年比上一年增加10%,那么2005年需退耕公顷。12.已知三个正数成等差数列,它们的和等于15,如果它们分别加上1,3,9,这三个数就又成为等比数列。①求出这三个数并写出由这三个数构成的等差数列的通项公式;②请写出题中的这个等比数列的一个通项公式.13.是否存在一个单调递增的等比数列,使其满足下列二个条件:①且;②至少存在一个,使依次成等差数列。若存在,写出数列的通项公式;若不存在,请说明理由。用心爱心专心