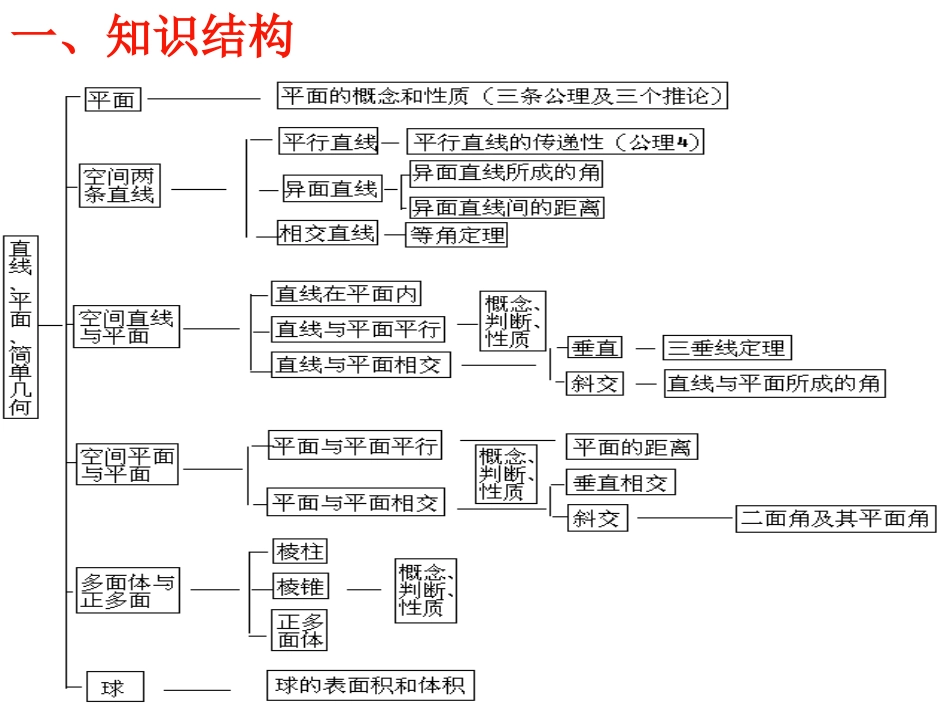
一、知识结构二、空间的直线与平面1:空间的角2:空间的距离3:平行与垂直直线与平面所成角直线与平面所成角平面与平面所成角平面与平面所成角异面直线所成的角异面直线所成的角解析:1(1)异面直线所成的角ABDCA1B1D1C1如:在正方体AC1中,求异面直线A1B和B1C所成的角?A1B和B1C所成的角为和A1B成角为60°的面对角线共有条。860°(2)线面角斜线与平面所成的角平面的一条斜线和它在这个平面内的射影所成的锐角BAO当直线与平面垂直时,直线与平面所成的角是90°当直线在平面内或与平面平行时,直线与平面所成的角是0°斜线与平面所成的角(0°,90°)直线与平面所成的角[0°,90°]异面直线所成的角(0°,90°]求直线与平面所成的角时,应注意的问题:(1)先判断直线与平面的位置关系(2)当直线与平面斜交时,常采用以下步骤:①作出或找出斜线上的点到平面的垂线②作出或找出斜线在平面上的射影③求出斜线段,射影,垂线段的长度④解此直角三角形,求出所成角的相应函数值(3)二面角从一条直线出发的两个半平面所形成的图形叫做二面角这条直线叫做二面角的棱二面角的平面角二面角的平面角以二面角的棱上任意一点为端点,以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角这两条射线所成的角叫做二面角的平面角O二面角的求法二面角的求法(1)垂线法——利用三垂线定理作出平面角,通过解直角三角形求角的大小(2)垂面法——通过做二面角的棱的垂面,两条交线所成的角即为平面角(3)射影法——若多边形的面积是S,它在一个平面上的射影图形面积是S`,则二面角的大小为COS=S`÷S垂线法ABCDO射影法解析2:空间距离两点之间的距离点到直线的距离、点到平面的距离两条平行线间的距离、两条异面直线间的距离、平面的平行直线与平面之间的距离两个平行平面之间的距离点—点点—线点—面线—线线—面点—面AH从平面外一点引这个平面的垂线垂足叫做点在这个平面内的射影这个点和垂足间的距离叫做点到平面的距离线面垂直点的射影点面距离线—面lA`A一条直线和一个平面平行时,直线上任意一点到这个平面的距离叫做直线到平面的距离lA`AlA`AB点—面线—面点到平面的距离的求法:(1)直接法即直接由点作垂线,求垂线段的长.(2)转移法转化成求另一点到该平面的距离.(3)体积法.解析3:平行与垂直直线在平面内直线和平面相交直线和平面平行线面位置关系有无数个公共点有且仅有一个公共点没有公共点位置关系图示表示方法公共点个数直线在平面内a无数个直线在平面外直线与平面相交斜交a一个垂直相交a一个直线与平面平行a无αaαaαAAaαa(1)定义——直线与平面没有公共点(2)定理——如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。线面平行的性质线面平行的性质(1)如果一条直线与一个平面平行,则这条直线与这个平面无公共点(2)如果一条直线与一个平面平行,则这条直线与这个平面内的直线成异面直线或平行直线(3)如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,则这条直线与交线平行。一、两个平面平行的判定方法1、两个平面没有公共点2、一个平面内有两条相交直线都平行于另一个平面3、都垂直于同一条直线的两个平面两个平面平行二、两个平面平行的性质4、一直线垂直于两个平行平面中的一个,则它也垂直于另一个平面2、其中一个平面内的直线平行于另一个平面3、两个平行平面同时和第三个平面相交,它们的交线平行两个平面平行5、夹在两个平行平面间的平行线段相等1、两个平面没有公共点线面垂直的判定方法(1)定义——如果一条直线和一个平面内的任意一条直线都垂直,则直线与平面垂直。(2)判定定理1——如果两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面。(3)判定定理2——如果一条直线和一个平面内的两条相交直线都垂直,则直线与平面垂直。线面垂直的性质(1)定义——如果一条直线和一个平面垂直则这条直线垂直于平面内的任意一条直线(2)性质定理——如果两条直线同垂直于一个平面...