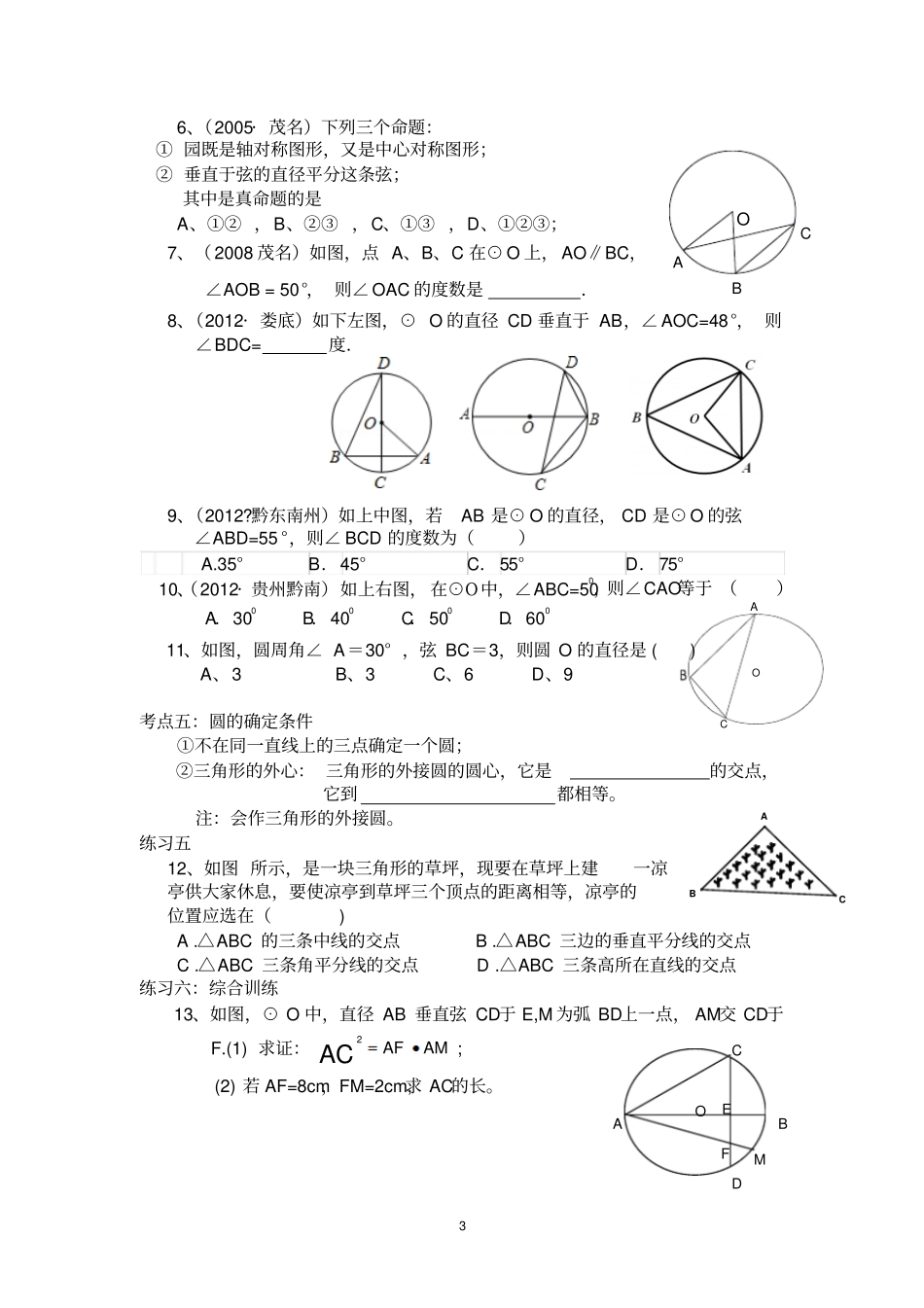
1a九年级数学复习(十四)《几何基础(2)--圆》姓名:第一部分:圆的有关性质考点一:圆的定义与性质(1)、圆的两要素:①,②。(2)、点与圆的位置关系:设⊙O的半径为r,点P到圆心O的距离为d,则:①、当dr时,点P在⊙O内部;②、当dr时,点P在⊙O上;③、当dr时,点P在⊙O外部。(反之也成立)(3)、圆是轴对称图形,对称轴是.(4)、圆是中心对称图形,对称中心是.(5)、圆具有旋转不变性,即圆绕圆心旋转任意角度,都能与原来图形.练习一1、在一个圆中任意引两条直径并顺次连结它们的四个端点组成一个四边形,则此四边形一定是()A.等腰梯形B.菱形C.矩形D.正方形考点二:垂径定理及推论(规律):①过圆心(直径),②垂直弦,③平分弦,④平分劣弧,⑤平分优弧。2个作条件,就可以得到其余的3个作结论。注:凡是解决与“弦、半径”有关的问题时,常常过圆心作垂线段(即弦心距),构成垂径定理或推论,最后转化为解直角三角形(如用勾股定理).规律:如图,⊙O的半径为r,弦CD的长为a,直径AB⊥CD,圆心O到弦CD的距离(弦心距)为h,弧CD的中点到弦的距离为d,则有关系式:①r2=②r=以上r、a、h、d四个量中,知道任意2个,由垂径定理或推论与直角三角形的勾股定理结合就可以求出其余的2个量。练习二2、(2012·茂名)如图,AB是⊙O的直径,CDAB于点E,若6CD,则DE()A.3B.4C.5D.63、(2012·湛江)如图,在半径为13的⊙O中,OC垂直弦AB于点B,交⊙O于点C,AB=24,则CD的长是.DACBEO(第2题图)24、(2012·六盘水)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为cm.5、(2008·茂名)如上中图,△ABC中,AB=AC=5,BC=6,⊙O是△ABC的外接圆,求⊙O半径的长为.考点三:圆心角、弧、弦之间关系定理在同圆或等圆中,两个圆心角,两条弦,两条弧,(两条弦的弦心距),只要有其中的一组量相等,那么其余各组量也相等。注:这是证明弦等或弧等或圆心角等的重要依据。如图1,A、B、C、D在⊙O上, ∠AOB=∠COD,∴、.考点四:圆周角定理与推论①圆周角定理:②一条弧所对的圆周角等于它所对的圆心角的。如图2,A、B、C在⊙O上, ∠AOB、∠ACB所对的弧是弧AB,(或弧AB=弧AB)∴、.②圆周角定理的推论:同弧或等弧所对的圆周角;如图3,A、B、D在⊙O上, 弧AB=弧AB∴、.如图4,A、B、C、D、E、F在⊙O上, 弧AB=弧CD∴、.直径(或半圆)所对的圆周角是;90度的圆周角所对的弦是。如图5,A、B、C在⊙O上, AB是⊙O的直径,∴.如图5,A、B、C在⊙O上, ∠ACB=900,∴.练习三AOBDCACBO图2ACDBO.图3.ABDCOEF图4ACBO图5ABCOD图13ACO6、(2005·茂名)下列三个命题:①园既是轴对称图形,又是中心对称图形;②垂直于弦的直径平分这条弦;其中是真命题的是A、①②,B、②③,C、①③,D、①②③;7、(2008茂名)如图,点A、B、C在⊙O上,AO∥BC,∠AOB=50°,则∠OAC的度数是.8、(2012·娄底)如下左图,⊙O的直径CD垂直于AB,∠AOC=48°,则∠BDC=度.9、(2012?黔东南州)如上中图,若AB是⊙O的直径,CD是⊙O的弦∠ABD=55°,则∠BCD的度数为()A.35°B.45°C.55°D.75°10、(2012·贵州黔南)如上右图,在⊙O中,∠ABC=500,则∠CAO等于()A.300B.400C.500D.60011、如图,圆周角∠A=30°,弦BC=3,则圆O的直径是()A、3B、3C、6D、9考点五:圆的确定条件①不在同一直线上的三点确定一个圆;②三角形的外心:三角形的外接圆的圆心,它是的交点,它到都相等。注:会作三角形的外接圆。练习五12、如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三个顶点的距离相等,凉亭的位置应选在()A.△ABC的三条中线的交点B.△ABC三边的垂直平分线的交点C.△ABC三条角平分线的交点D.△ABC三条高所在直线的交点练习六:综合训练13、如图,⊙O中,直径AB垂直弦CD于E,M为弧BD上一点,AM交CD于F.(1)求证:AMAFAC2;(2)若AF=8cm,FM=2cm,求AC的长。FMDCOABEBCAOCBA4ABCOOPBAC14、如图,已知A、B、C、D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD.(1)求证:DB平分∠ADC;...