人工智能_贝叶斯网络VIP免费

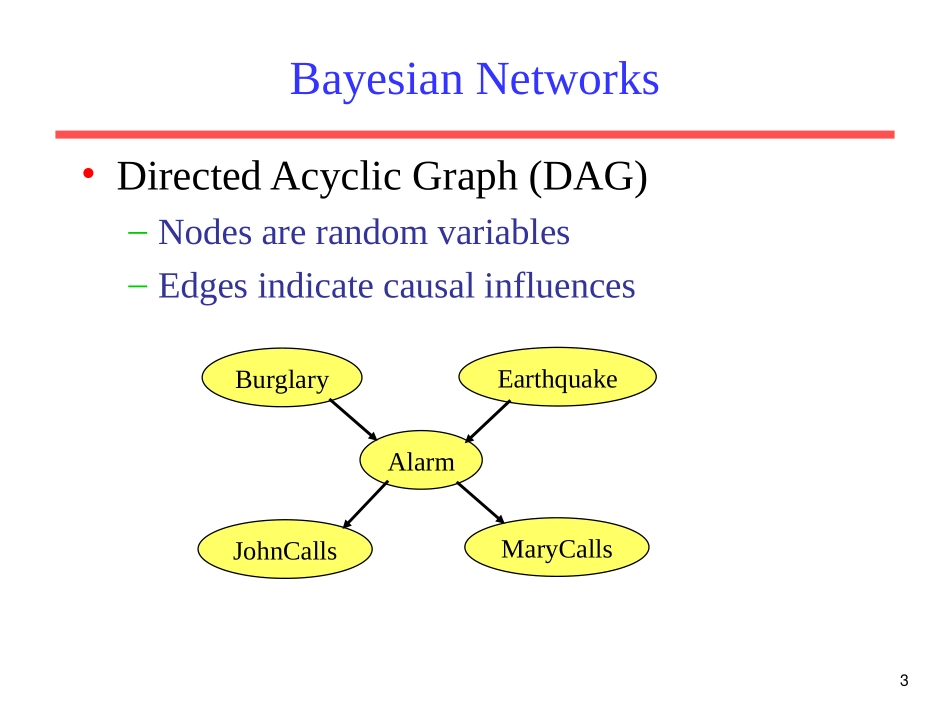
1ArtificialIntelligence:BayesianNetworks2GraphicalModels•Ifnoassumptionofindependenceismade,thenanexponentialnumberofparametersmustbeestimatedforsoundprobabilisticinference.•Norealisticamountoftrainingdataissufficienttoestimatesomanyparameters.•Ifablanketassumptionofconditionalindependenceismade,efficienttrainingandinferenceispossible,butsuchastrongassumptionisrarelywarranted.•Graphicalmodelsusedirectedorundirectedgraphsoverasetofrandomvariablestoexplicitlyspecifyvariabledependenciesandallowforlessrestrictiveindependenceassumptionswhilelimitingthenumberofparametersthatmustbeestimated.–BayesianNetworks:Directedacyclicgraphsthatindicatecausalstructure.–MarkovNetworks:Undirectedgraphsthatcapturegeneraldependencies.3BayesianNetworks•DirectedAcyclicGraph(DAG)–Nodesarerandomvariables–EdgesindicatecausalinfluencesBurglaryEarthquakeAlarmJohnCallsMaryCalls4ConditionalProbabilityTables•Eachnodehasaconditionalprobabilitytable(CPT)thatgivestheprobabilityofeachofitsvaluesgiveneverypossiblecombinationofvaluesforitsparents(conditioningcase).–Roots(sources)oftheDAGthathavenoparentsaregivenpriorprobabilities.BurglaryEarthquakeAlarmJohnCallsMaryCallsP(B).001P(E).002BEP(A)TT.95TF.94FT.29FF.001AP(M)T.70F.01AP(J)T.90F.055CPTComments•Probabilityoffalsenotgivensincerowsmustaddto1.•Examplerequires10parametersratherthan25–1=31forspecifyingthefulljointdistribution.•NumberofparametersintheCPTforanodeisexponentialinthenumberofparents(fan-in).6JointDistributionsforBayesNets•ABayesianNetworkimplicitlydefinesajointdistribution.))(Parents|(),...,(121iniinXxPxxxP•Example)(EBAMJP)()()|()|()|(EPBPEBAPAMPAJP00062.0998.0999.0001.07.09.0•Thereforeaninefficientapproachtoinferenceis:–1)Computethejointdistributionusingthisequation.–2)Computeanydesiredconditionalprobabilityusingthejointdistribution.7NaïveBayesasaBayesNet•NaïveBayesisasimpleBayesNetYX1X2…Xn•PriorsP(Y)andconditionalsP(Xi|Y)forNaïveBayesprovideCPTsforthenetwork.8IndependenciesinBayesNets•IfremovingasubsetofnodesSfromthenetworkrendersnodesXiandXjdisconnected,thenXiandXjareindependentgivenS,i.e.P(Xi|Xj,S)=P(Xi|S)•However,thisistoostrictacriteriaforconditionalindependencesincetwonodeswillstillbeconsideredindependentiftheirsimplyexistssomevariablethatdependsonboth.–Forexample,BurglaryandEarthquakeshouldbeconsideredindependentsincetheybothcauseAlarm.9IndependenciesinBayesNets•IfremovingasubsetofnodesSfromthenetworkrendersnodesXiandXjdisconnected,thenXiandXjareindependentgivenS,i.e.P(Xi|Xj,S)=P(Xi|S)•However,thisistoostrictacriteriaforconditionalindependencesincetwonodeswillstillbeconsideredindependentiftheirsimplyexistssomevariablethatdependsonboth.–Forexample,BurglaryandEarthquakeshouldbeconsideredindependentsincetheybothcauseAlarm.P(Xi|Xj,S)=P(Xi|S),isequivalenttoP(Xi,Xj|S)=P(Xi|S)P(Xj|S)Howtoprove?10IndependenciesinBayesNets•IfremovingasubsetofnodesSfromthenetworkrendersnodesXiandXjdisconnected,thenXiandXjareindependentgivenS,i.e.P(Xi|Xj,S)=P(Xi|S)•However,thisistoostrictacriteriaforconditionalindependencesincetwonodeswillstillbeconsideredindependentiftheirsimplyexistssomevariablethatdependsonboth.–Forexample,BurglaryandEarthquakeshouldbeconsideredindependentsincetheybothcauseAlarm.11IndependenciesinBayesNets(cont.)•Unlessweknowsomethingaboutacommoneffectoftwo“independent...