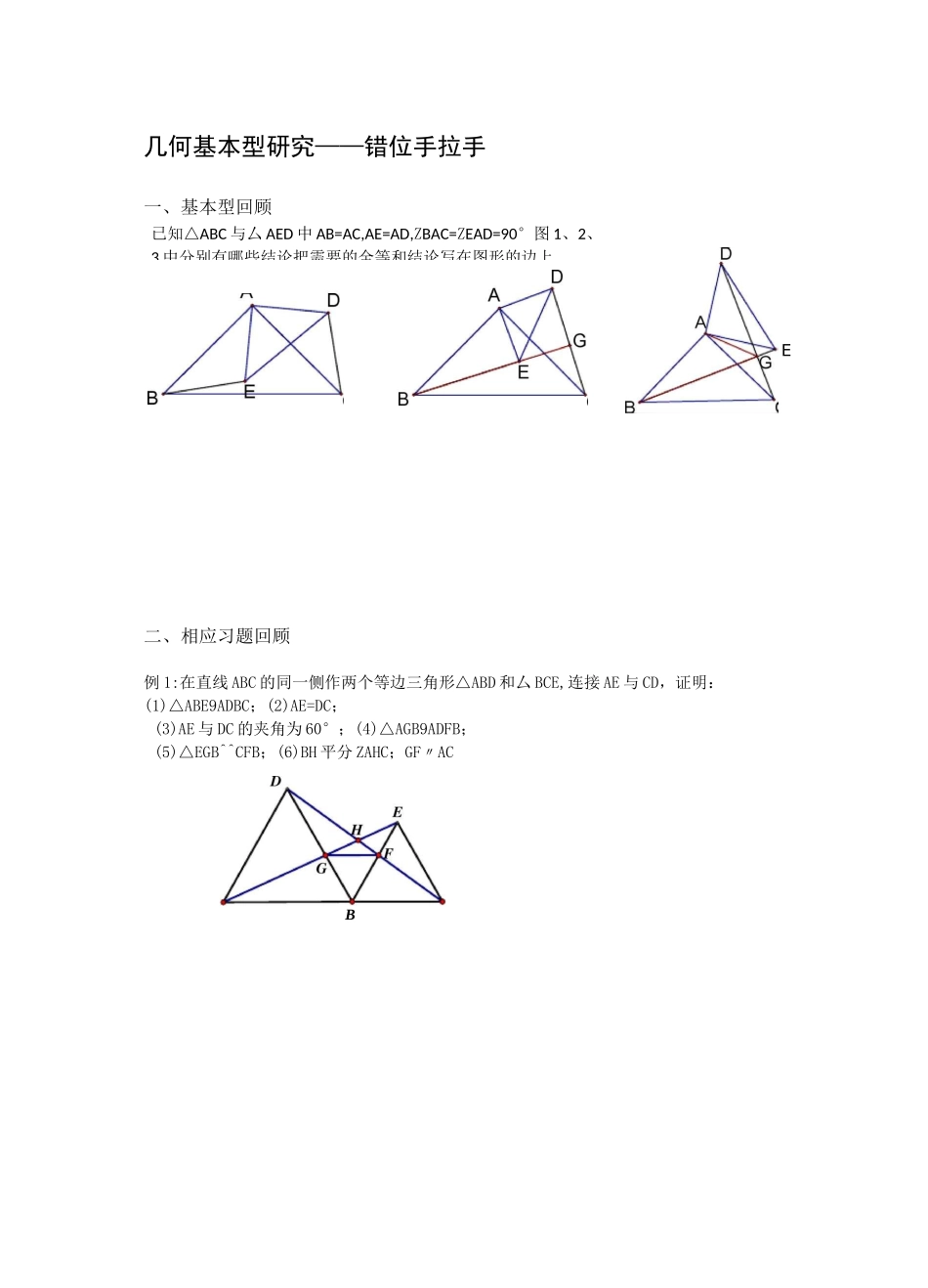
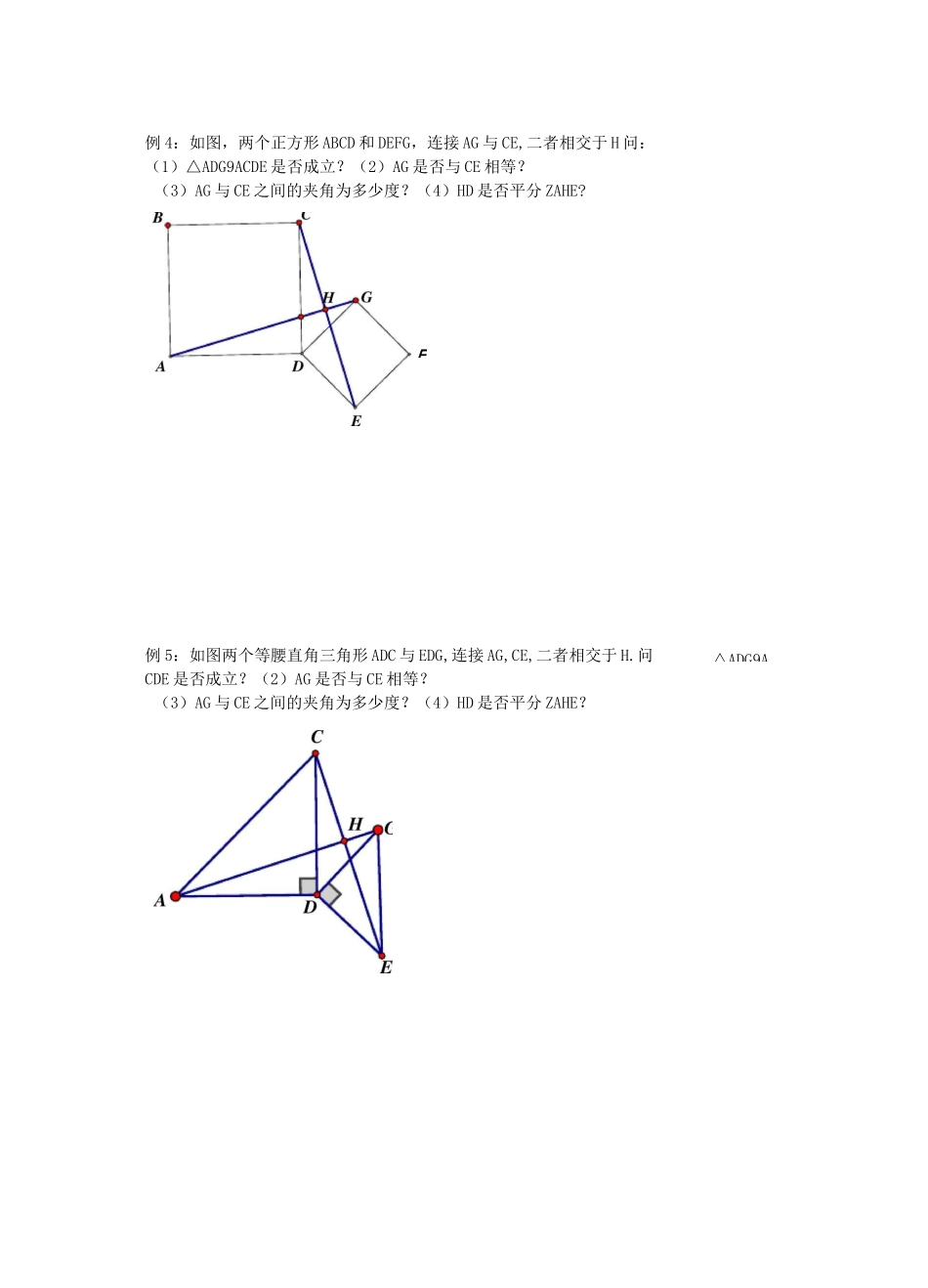
已知△ABC与厶AED中AB=AC,AE=AD,ZBAC=ZEAD=90°图1、2、3中分别有哪些结论把需要的全等和结论写在图形的边上.几何基本型研究——错位手拉手一、基本型回顾二、相应习题回顾例1:在直线ABC的同一侧作两个等边三角形△ABD和厶BCE,连接AE与CD,证明:(1)△ABE9ADBC;(2)AE=DC;(3)AE与DC的夹角为60°;(4)△AGB9ADFB;(5)△EGB^^CFB;(6)BH平分ZAHC;GF〃ACEBC例2:如果两个等边三角形△ABD和厶BCE,连接AE与CD,证明:(1)△ABE9ADBC;(2)AE=DC;(3)AE与DC的夹角为60°;(4)AE与DC的交点设为H,BH平分ZAHC例3:如果两个等边三角形△ABD和厶BCE,连接AE与CD,证明:(1)△ABE^^DBC;(2)AE=DC;(3)AE与DC的夹角为60°;(4)AE与DC的交点设为H,BH平分ZAHCD△ADG9A例4:如图,两个正方形ABCD和DEFG,连接AG与CE,二者相交于H问:(1)△ADG9ACDE是否成立?(2)AG是否与CE相等?(3)AG与CE之间的夹角为多少度?(4)HD是否平分ZAHE?例5:如图两个等腰直角三角形ADC与EDG,连接AG,CE,二者相交于H.问CDE是否成立?(2)AG是否与CE相等?(3)AG与CE之间的夹角为多少度?(4)HD是否平分ZAHE?FDFC例6.两个等腰三角形ABD与BCE,其中AB=BD,CB=EB,ZABD=ZCBE=a,连接AE与CD.问(1)△ABE9ADBC是否成立?(2)AE是否与CD相等?(3)AE与CD之间的夹角为多少度?(4)HB是否平分ZAHC?7.在厶ABC中,AB=AC,ZBAC=90°,点D在CB上,连接AD,EA丄AD,ZACE=ZABD.若点F为CD中点,AF交BE于点G,ZCBE=15°,AG=3V2则BC的长为.图■图在平面直角坐标系中”出的坐扳賢别为{2卫)亿0}卫农什别往*轴的负半轴,了轴的负半轴Al,AO=CO=rhl,E在射线腮上仰JJT轴于F是感的面积为25.(1)如图「求2;点的坐标;估)如图厶动点6;从£点出发1个单竝徂秒遞度向蜓点F运动,设f?运动吋间为丄秒丄&關的面积为乩用0戟示S,井直接写出*范围;⑶如倒孔在⑵的条件下也为DE的中点准接ME柞械丄磁交EF于凰H,连接眄过M作嗣Q丄EG近EF于点Q,当QH:^=3:4时,求氏>的底度井求出ftl应的土值.三、错位手拉手基本型初探已知△ABC与乂AED中AB=AC,AE=AD,ZBAC=ZEAD=90。连接BD、CE,AF交BD于F,交EC于G.⑴若G是EC中点,求证:AF垂直BD⑵若AF垂直BD,求证:EG=GC.⑶若G是BE中点求证:AF丄CD⑷若AF丄CD求证:BG=GE四、基本型旋转再探⑸若G是CE中点求证:AF丄BD⑹若AF丄BD求证:CG=GEB五、方法迁移如图1、已知AABC是等边三角形,AADE中AD=AE,且ZDAE=120。连接BE、DC,BE、DC交于点H,G是DC中点连接AG并延长交BC于点P,求证AH=PC如图2已知△ABC是等边三角形,AADE中AD=AE,且ZDAE=120。连接BE、DC.Q是BE中点连接AQ并延长交DC于点R,若AD丄DC,求证:AR=2DR