正弦定理第课时VIP免费

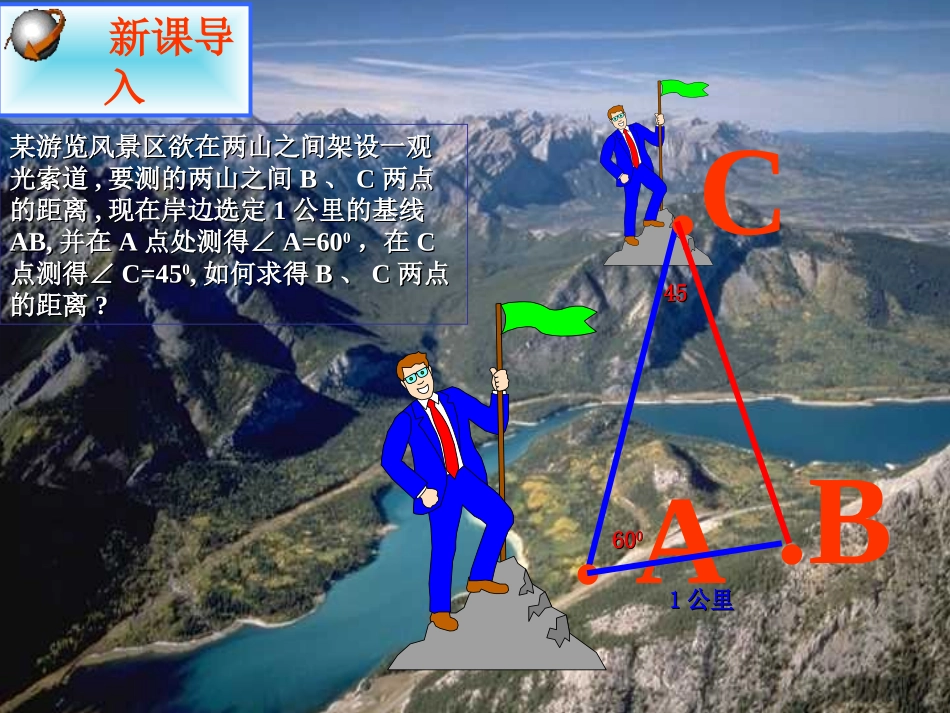
第一章解三角形.B某游览风景区欲在两山之间架设一观某游览风景区欲在两山之间架设一观光索道光索道,,要测的两山之间要测的两山之间BB、、CC两点两点的距离的距离,,现在岸边选定现在岸边选定11公里的基线公里的基线AB,AB,并在并在AA点处测得∠点处测得∠A=60A=6000，在，在CC点测得∠点测得∠C=45C=4500,,如何求得如何求得BB、、CC两点两点的距离的距离??.C新课导入6060004545.A11公里公里复习三角形中的边角关系180CBAcbacba,大角对大边1、角的关系2、边的关系3、边角关系（一）任意三角形中的边角关系（二）直角三角形中的边角关系（角C为直角）1、角的关系2、边的关系3、边角关系90BA222cba复习引入ABCabc探索：直角三角形的边角关系式对任意三角形是否成立？1sin,sin,sinCcbBcaACcBbAasinsinsin复习引入即直角三角形中的边角关系,sinAac,sinCcc,sinBbc,1sinccC所以asinB=bsinA,得到.sinsinBbAa.sinsinCcBb同理，在ABC中，ABCcba如图，当ABC是锐角三角形时，锐角三角形D设边AB上的高是CD，根据三角函数的定义，CD=asinB,CD=bsinA,CcBbAasinsinsin所以构造直角三角形探究论证ABCcbaD钝角三角形注意：同样是构造直角三角形来解次这一问题。CcBbAasinsinsin所以BbAasinsin所以同理CcBbsinsin探究论证BaCDsin)sin(AbAbsin由以上推论可知：对于作何三角形而言，都有：三角形各边和其所对角的正弦值之比相等,即CcBbAasinsinsin这就是正弦定理归纳总结CcBbAasinsinsin正弦定理在一个三角形中，各边和它所对角的正弦的比相等，即归纳总结1CCABCC1abcO如图:RCcCc2sinsin1RAaRBb2sin2sin，同理：为外接圆半径即得：RRCcBbAa2sinsinsin一题多证向量的数量积，为向量a与b的夹角．cos||||baba如何构造向量及等式？jACB在锐角中，过A作单位向量j垂直于，ACABC则有j与的夹角为，j与的夹角为.等式A90CBC90ABCBACAB怎样建立三角形中边和角间的关系？ABjCBACj)()90cos()90cos(90cosAABjCCBjACjAcCasinsin即CcAasinsin同理，过C作单位向量j垂直于，可得CBCcBbsinsin一题多证CcBbAasinsinsin在钝角三角形中，怎样将三角形的边用向量表示？怎样引入单位向量？怎样取数量积？jACB在钝角中，过A作单位向量j垂直于，ACABC则有j与的夹角为，j与的夹角为.等式.90ACBC90ABCBACAB同样可证得：CcBbAasinsinsin一题多证CcBbAasinsinsin正弦定理在一个三角形中，各边和它所对角的正弦的比相等，即总结归纳正弦定理可以解什么类型的三角形问题？（1）已知两角和任意一边，可以求出其他两边和一角；（2）已知两边和其中一边的对角，可以求出三角形的其他的边和角。注：有了正弦定理，前面的设问可就比较容易解决了。一般地，把三角形的三个角A，B，C，及其对边a，b，c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫解三角形。三角形的边和角我们也称为三角形的“元素”。解三角形：______,3,3,6,,,,,,)1(aCcAcbaCBAABC则若所对的边分别为角中在牛刀小试1（2）在中，一定成立的等式是（）ABCBbAaA.sinsinBbAaBcoscos.AbBaC.sinsinAbBaDcoscos.C3sin6sinca23321a1aBbAasinsin例1在中，已知，求。ABC45,24,4BbaA解：由BbAasinsin得21sinsinbBaA 在中ABCba∴A为锐角30A例题讲解类型：已知两边和其中一边的对角,求其他边或角。注意：大边对大角!例2：已知a=16，b=，A=30°.求角B，C和边c。类型：已知两边和其中一边的对角,求其他边或角。解：BbAasinsin有231630sin316sinsinaAbB所以Ｂ＝60°,或Ｂ＝120°316由正弦定理例题讲解当时，Ｂ＝60°C=90°，.32cC=30°，.16sinsinACac当Ｂ＝120°时，300ABC16316300ABC16316例题讲解注意：学会分类!练习：1.在CAacBbABC,,1,60,30和求中，课堂练习00090,30,,60,ACCBCBcb为锐角，∴222cba解 21360sin1sinsin,sinsin0bBcCCcBb注...