【精品课件】111正弦定理VIP免费

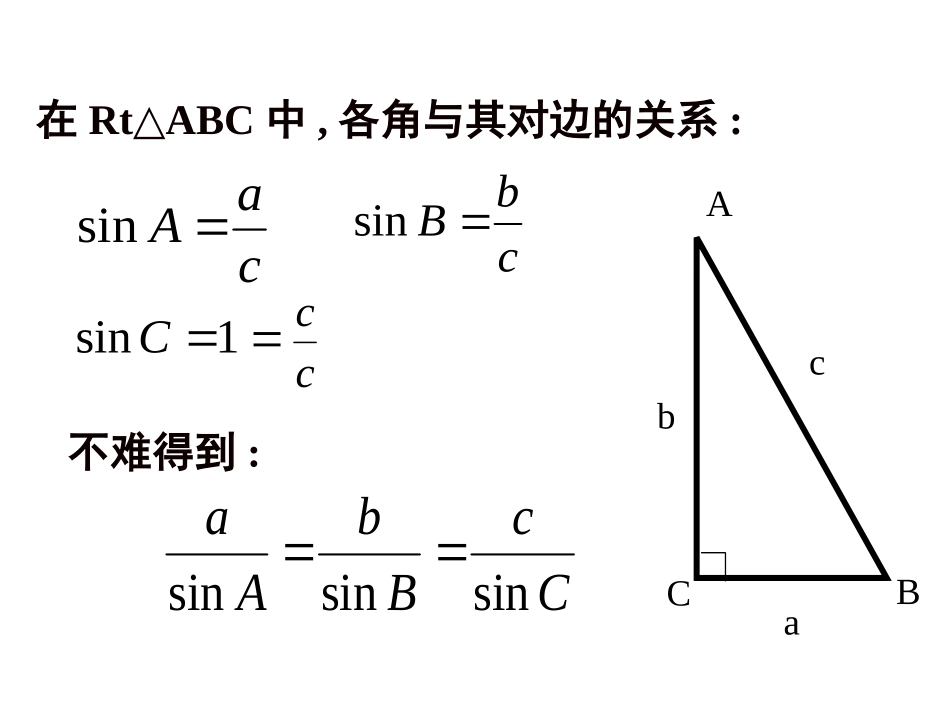
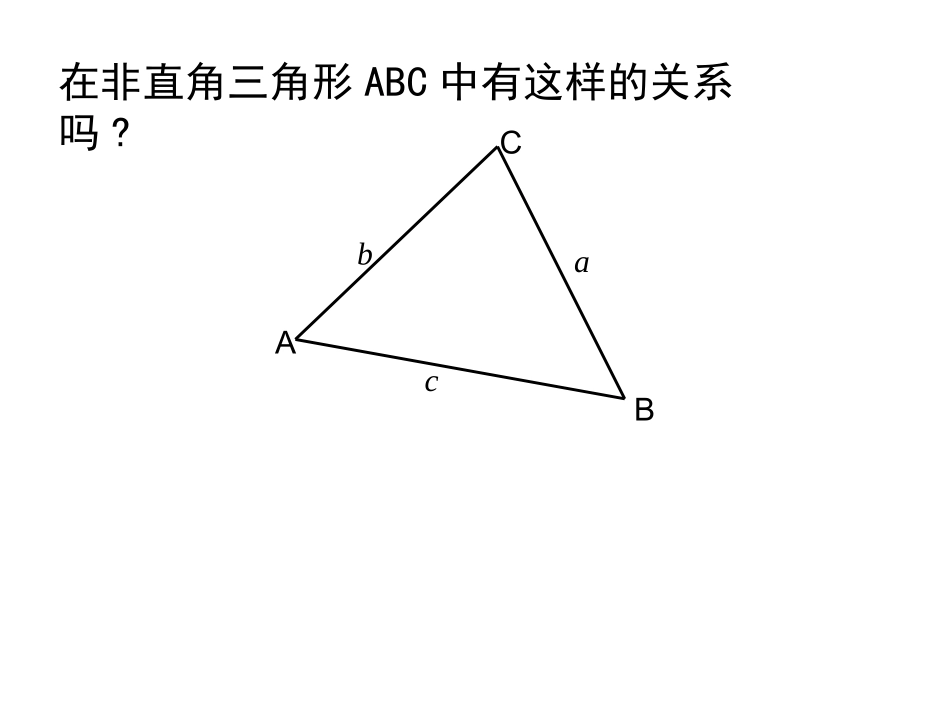
正弦定理罗田县第一中学杨远中在RtABC△中,各角与其对边的关系:caAsincbBsin1sinC不难得到:CcBbAasinsinsinCBAabccc在非直角三角形ABC中有这样的关系吗?AcbaCBbADcADCBsin,sin所以AD=csinB=bsinC,即,sinsinCcBb同理可得,sinsinCcAasinsinsinabcABC即：DAcbCB图1过点A作ADBC⊥于D,此时有(1)若三角形是锐角三角形,如图1,(2)若三角形是钝角三角形呢？自己证下！正弦定理:在一个三角形中,各边和它所对角的正弦的比相等.CcBbAasinsinsin即即正弦定理寻找的是各边和它的对角的关系！剖析定理、加深理解正弦定理可以解决三角形中哪类问题：①已知两角和一边，求其他角和边.②已知两边和其中一边的对角，求另一边的对角，进而可求其他的边和角.CcBbAasinsinsin定理的应用例1：在△ABC中，已知c=10,A=45。,C=30。，解三角形.（即求出其它边和角）解：B180(AC)105sinsinbcBC由正弦定理得b=CBcsinsin=30sin105sin10（1）已知两角和任一边，求其他两边和一角sinsinacAC由正弦定理sinsincAaC得=21030sin45sin10BACbc)26(5a根据三角形内角和定理，（2）在△ABC中，已知A=75°，B=45°，c=求C，a，b.23（1）在△ABC中，已知A=30°，B=120°，b=12。解三角形.30,43Cac练习：已知两角和任一边，求其他两边和一角.60,33,23Cab0,2,45,,,ABCbBACc例2：在中，a=3求00,,0180abABA且060A000(1)60,180()75ACAB当sin26262sin4222bCcB000(2)120,180()15ACAB当sin26262sin4222bCcB23sin32sin22aBAb解：(2)已知两边和其中一边的对角,求其他边和角.0120A或（三角形中大边对大角）0,2,45,,,ABCbACc练习：在中，a=2求B22sin12sin22bABa解：由正弦定理得00,,0180abABB且030,105BCsin26231sin422aCcA(2)已知两边和其中一边的对角,求其他边和角.（三角形中大边对大角）课堂小结（1）三角形常用公式：（2）正弦定理应用范围：①已知两角和任意边，求其他两边和一角②已知两边和其中一边的对角，求另一边的对角。(注意解的情况)正弦定理：ABCsinsinsinabcABC正弦定理推广一:外接圆半径是ABCRR2CsincBsinbAsina证明：OC/cbaCBARCcRcCCCCCBA2sin2sinsin,90''RCcBbAaRBbRAa2sinsinsin2sin,2sin同理作外接圆O,过B作直径BC/,连AC/,应用正弦定理化边为角：2sin,2sin,2sinaRAbRBcRC或化角为边：sin,sin,sin222abcABCRRR正弦定理：sinsinsinabcABC＝2R公式的应用课堂练习：002.2,7545______.sinsinsinABCaBCabcABC已知中，，则231：：3、已知三角形ABC中，acosA=bcosB,判断三角形的形状。直角或等腰三角形1.::3:2:1,::____________ABCABCabc已知的三个内角之比为那么对应的三边之比等于334Asinbc21Bsinac21Csinab21ah21S:ABC正弦面积公式正弦定理推广二:1.,6845.______.ABCABCabCS在中，，则2.已知三角形ABC中，a=50,B=450,C=1050,求ABCS.练习：12262531（）3.(2008全国Ⅱ)在ABC△中，5cos13A，3cos5B．（Ⅰ）求sinC的值；（Ⅱ）设5BC，求ABC△的面积．3．解：（Ⅰ）由5cos13A，得12sin13A，由3cos5B，得4sin5B．所以16sinsin()sincoscossin65CABABAB．3.(2008全国Ⅱ)在ABC△中，5cos13A，3cos5B．（Ⅰ）求sinC的值；（Ⅱ）设5BC，求ABC△的面积．（Ⅱ）由正弦定理得45sin13512sin313BCBACA．所以ABC△的面积1sin2SBCACC113165236583．4.,3,1,30,__________ABCabB在中则其面积等于3324或AasinBbsinCcsin＝＝（2R为△ABC外接圆直径）＝？2R思考5、求证:证明：∵111sinsinsin222ABCSabCbcAacBBACDabcaABCahS21而CbBcADhasinsin∴CabBacSABCsin21sin21同理∴BacAbcCabSABCsin21sin21sin21haAbcSABCsin21证法3:2.（08陕西卷）ABC△的内角ABC，，的对边分别为abc，，，若26120cbB，，，则a等于（）A．6B．2C．3D．2D(2)已知两边和其中一边的对角,求其他边和角.ABC3C2C1CBC的长度与角A的大小有关吗?三角形中角A与它的对边BC的长度是否存在数量关系?由(1)(2)知，结论成立．CCbADsinsin）（且sinsinsinabcABC仿(1)可得D(2)若三角形是钝角三角形,且角C是钝角如图2,此时也有cADBsin交BC延长线于D,过点A作ADBC⊥，CAcbB图2AasinBbsinCcsin＝＝（2R为△ABC外接圆直径）＝？2R思考求证: