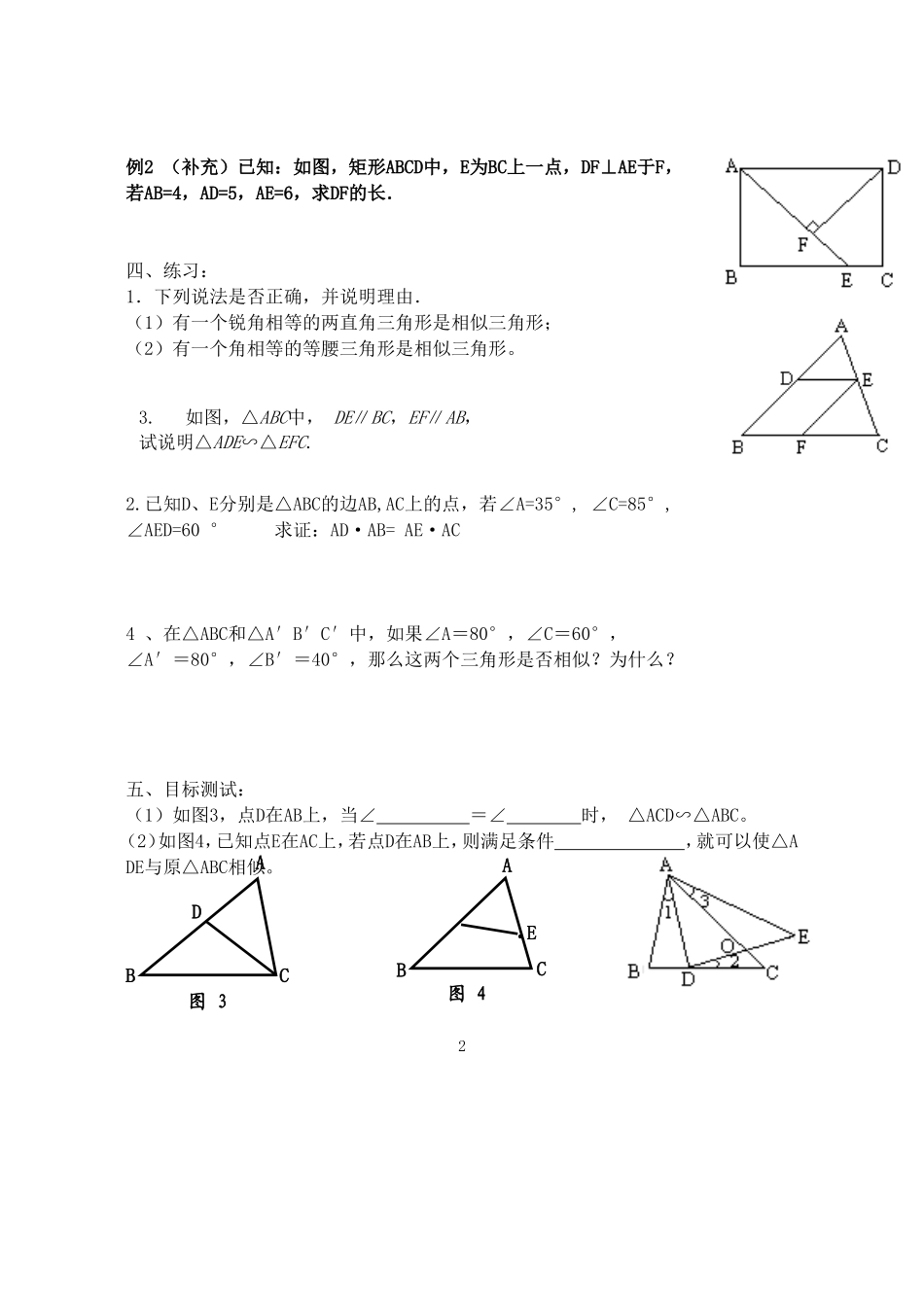
老河口市四中目标学案相似三角形的判定4课型:新授时间:2010。11。30执笔:李华审核:孙梅一、学习目标1.掌握“两角对应相等,两个三角形相似”的判定方法.2.能够运用三角形相似的条件解决简单的问题.重点:三角形相似的判定方法3——“两角对应相等,两个三角形相似”难点:三角形相似的判定方法3的运用.二、知识链接(1)我们已学习过哪些判定三角形相似的方法?(2)如图,△ABC中,点D在AB上,如果AC2=AD•AB,那么△ACD与△ABC相似吗?说说你的理由.3)如(2)题图,△ABC中,点D在AB上,如果∠ACD=∠B,那么△ACD与△ABC相似吗?三角形相似的判定方法3如果一个三角形的两个角与另一个三角形两个角对应相等,那么这两个三角形相似.三、例题讲解例1(教材P48例2).弦AB和CD相交于⊙o内一点P,求证:PAPB=PCPD分析:要证PA•PB=PC•PD,需要证,则需要证明这四条线段所在的两个三角形相似.由于所给的条件是圆中的两条相交弦,故需要先作辅助线构造三角形,然后利用圆的性质“同弧上的圆周角相等”得到两组角对应相等,再由三角形相似的判定方法3,可得两三角形相似.1ABCDPO例2(补充)已知:如图,矩形ABCD中,E为BC上一点,DF⊥AE于F,若AB=4,AD=5,AE=6,求DF的长.四、练习:1.下列说法是否正确,并说明理由.(1)有一个锐角相等的两直角三角形是相似三角形;(2)有一个角相等的等腰三角形是相似三角形。2.已知D、E分别是△ABC的边AB,AC上的点,若∠A=35°,∠C=85°,∠AED=60°求证:AD·AB=AE·AC4、在△ABC和△A′B′C′中,如果∠A=80°,∠C=60°,∠A′=80°,∠B′=40°,那么这两个三角形是否相似?为什么?五、目标测试:(1)如图3,点D在AB上,当∠=∠时,△ACD∽△ABC。(2)如图4,已知点E在AC上,若点D在AB上,则满足条件,就可以使△ADE与原△ABC相似。2ABDC图3●ABCE图43.如图,△ABC中,DE∥BC,EF∥AB,试说明△ADE∽△EFC.3.已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.4、已知:如图,△ABC的高AD、BE交于点F.1).找出所有的相似三角形2).求证:.考点一角:已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.(1)求证:AC•BC=BE•CD;(2)若CD=6,AD=3,BD=8,求⊙O的直径BE的长.教学后记:3