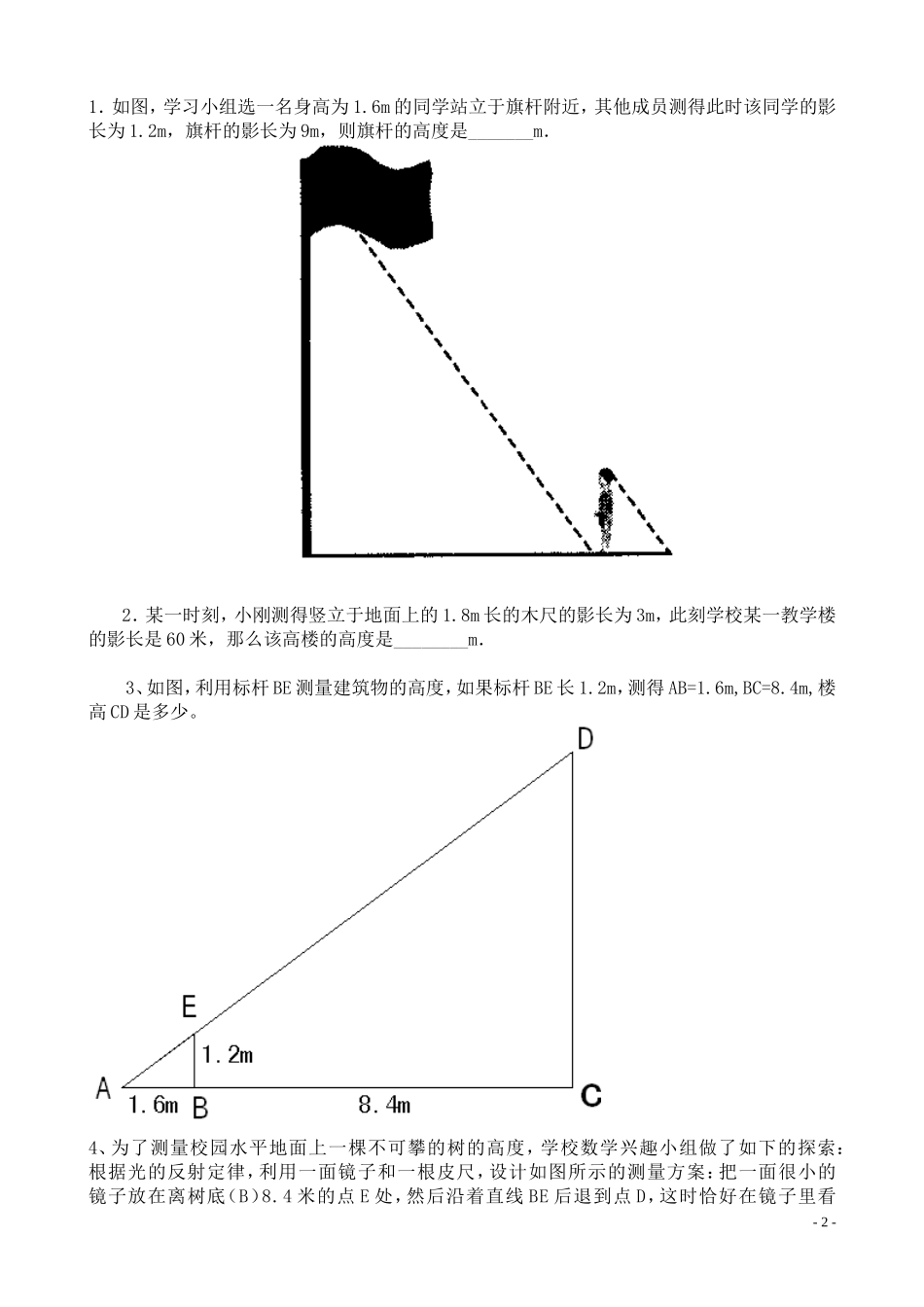
27.2.2相似三角形的应用———测物高教学目标:1.进一步巩固相似三角形的知识.2.能够运用三角形相似的知识,解决不能直接测量物体的高度(如测量金字塔高度问题等)的一些实际问题.3.通过把实际问题转化成有关相似三角形的数学模型,进一步了解数学建模的思想,培养学生分析问题、解决问题的能力.教学重点:运用三角形相似的判定及性质计算不能直接测量物体的高度.教学难点:运用相似三角形的判定定理构造相似三角形解决实际问题。关键:将实际问题转化为相似三角形的数学模型,利用所学的知识来进行解答。一、课前回顾:1.相似三角形的对应角______,对应边的比______.2.若△ABC与△A′B′C′相似,一组对应边的长为AB=3cm,A′B′=4cm,那么△A′B′C′与△ABC的相似比是________3.下列命题错误的是()A.两个全等的三角形一定相似B.两个相似三角形的对应角相等,对应边成比例C.两个直角三角形一定相似D.相似的两个三角形不一定全等4.相似三角形的判定方法有。5.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高_____m?二、探索新知了解平行光线自无穷远处发的光相互平行地向前行进,称平行光。自然界中最标准的平行光是太阳光。现在给你一根竹竿,一把皮尺,你能测量出金字塔的高度吗?问题一:如何测高度在金字塔影子的顶部立一根本杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度。如果木杆EF长2m,它的影长FD为3m,测得OA为201m,求金字塔的高度BO.思考:(1)太阳光线BA、ED之间有什么关系?(2)△ABO和△DEF有什么特殊关系?(3)由EF=2m,FD=3m,OA=201m,怎样求BO?三、巩固和拓展-1-1.如图,学习小组选一名身高为1.6m的同学站立于旗杆附近,其他成员测得此时该同学的影长为1.2m,旗杆的影长为9m,则旗杆的高度是_______m.2.某一时刻,小刚测得竖立于地面上的1.8m长的木尺的影长为3m,此刻学校某一教学楼的影长是60米,那么该高楼的高度是________m.3、如图,利用标杆BE测量建筑物的高度,如果标杆BE长1.2m,测得AB=1.6m,BC=8.4m,楼高CD是多少。4、为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看-2-到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度是多少米?5、小明要测量一座古塔的高度,从距他2米的一小块积水处C看到塔顶的倒影,已知小明的眼部离地面的高度DE是1.5米,塔底中心B到积水处C的距离是40米.求塔高AB?五、小结:如何把一些实际问题抽象为三角形相似的数学问题六、作业:1.练习册:35-36-3-C