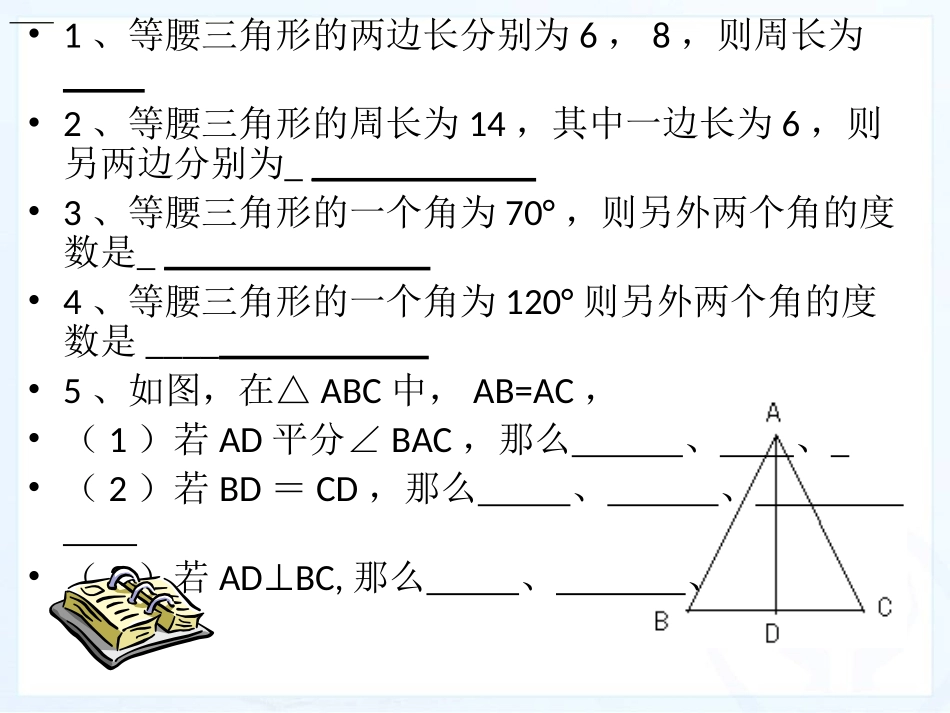
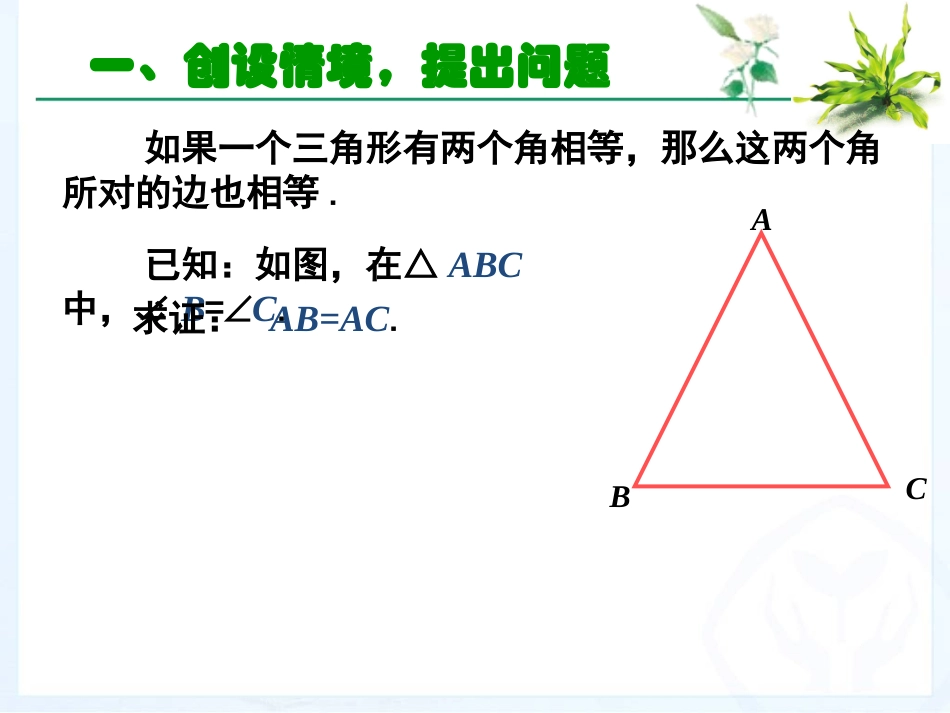
13.3等腰三角形(第2课时)八年级上册•1、等腰三角形的两边长分别为6,8,则周长为____•2、等腰三角形的周长为14,其中一边长为6,则另两边分别为____•3、等腰三角形的一个角为70°,则另外两个角的度数是____•4、等腰三角形的一个角为120°则另外两个角的度数是____•5、如图,在△ABC中,AB=AC,•(1)若AD平分∠BAC,那么、、•(2)若BD=CD,那么、、•(3)若ADBC,⊥那么、、如果一个三角形有两个角相等,那么这两个角所对的边也相等.ACB已知:如图,在△ABC中,∠B=C.求证:AB=AC.一、创设情境,提出问题二、探索分析,解决问题分析:类比等腰三角形性质的证明,添加辅助线,构造以AC,AB为边的两三角形,并证明它们全等.ACB证明:过点A作AD⊥BC于D.在△ABD与△ACD中,∠B=∠C,∠ADB=∠ADC=90°,AD=AD,∴△ABD≌△ACD(AAS),∴AB=AC.D你还有其他证法吗?ABC如果一个三角形有两个角相等,那么这两个角所对的边也相等几何语言:∵∠B=∠C(已知)∴AB=AC(等角对等边)等腰三角形的判定定理:(简写成“等角对等边”)。注意:在同一个三角形中应用哟!例1:求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。已知:∠CAE是∆ABC的外角,∠1=∠2,AD//BC,(如图),求证:AB=AC。证明:∵AD//BC∴∠1=∠B∴∠2=∠C又已知∠1=2∠∴∠B=∠CAB=AC(_______________________)(_____________________________)(____________________)两直线平行,内错角相等等角对等边两直线平行,同位角相等CABDE12合作探究1如图,AC和BD相交于点O,且AB∥DC,OA=OB.求证:OC=OD.ABCDO能力提升三、应用举例,变式练习2求证:如果三角形一条边上的中线等于这条边上的一半,那么这个三角形是直角三角形.DC巩固等腰三角形的判定定理例2已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形.ah作法:(1)作线段AB=a;(2)作线段AB的垂直平分线MN,与AB相交于点D;(3)在MN上取一点C,使DC=h;(4)连接AC,BC,则△ABC就是所求作的等腰三角形.ABMNDCABBFDECAACBFEO1、如图,△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F求证:EF=EB+FC.2、如图,ADBC∥,BD平分∠ABC.求证:AB=AD.3、如图,∠A=∠B,CEDA∥,CE交AB于E,求证△CEB是等腰三角形4、E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE。求证:△ABC是等腰三角形选做题:①P是等腰三角形底边BC上的一点,过P作PQ⊥BC交AB于Q,交CA的延长线于R,求证:△AQR是等腰三角形.②当P在直线CB上时,其它条件不变,将图形补充完整①中的结论成立吗?RACPBQPBCAABCD2、如图,∠A=36°,AB=AC,BD平分∠ABC,则图中一共有__个等腰三角形.3、条件同上,若CE也平分∠ACB,交BD于O,则图中等腰三角形有__个.达标检测基础训练1、已知一个三角形的两个内角为50°和80°,则第三个角为__,它是三角形___.在△ABC中,AB=AC,∠B=90°,点D、E分别是AB、BC边上的动点,且BD与CE相等,点M是AC的中点,试探究在D、E运动过程中,△DEM的形状是否发生变化,它是什么形状的三角形?ADBECM能力提升小结名名称称图图形形概念概念性质性质判判定定等等腰腰三三角角形形ABC有两边相等的三角形是等腰三角形2.等边对等角3.三线合一4.是轴对称图形2.等角对等边1.两边相等1.两腰相等运用等腰三角形的判定定理时,应注意在同一个三角形中.教科书习题82页,2、5题.布置作业