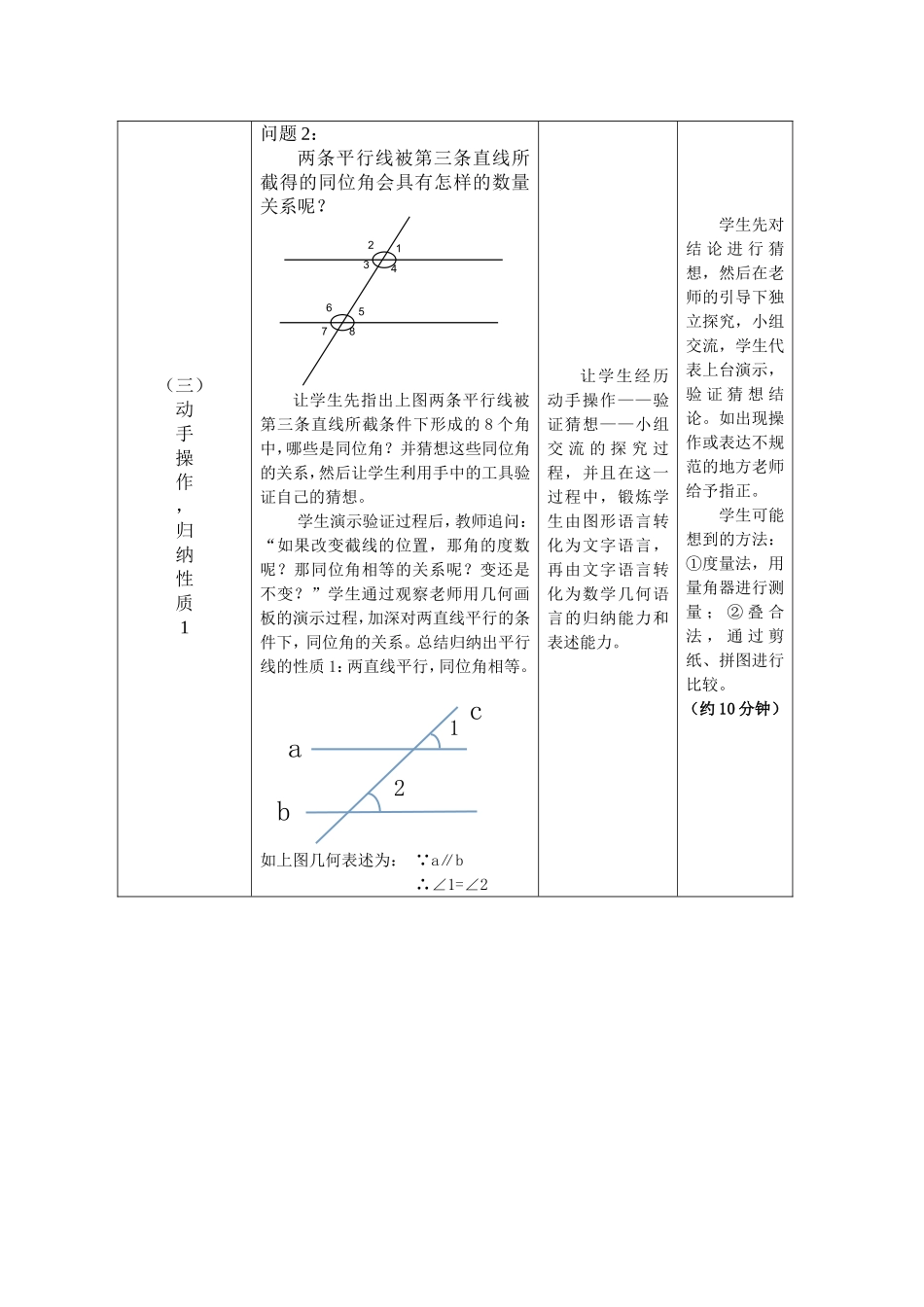
七年级数学下册第五章5.3《平行线的性质》教学设计【教学目标】知识与技能:探索平行线的性质,并会运用性质进行简单推理;了解平行线的性质和判定的区别。过程与方法:通过学生动手操作、观察、小组交流,确认获得性质1,再借助已有的相关知识,通过推理得到另外两条性质。情感态度价值目标:情境的创设,使学生认识到数学来源于生活又服务于生活,从而认识到数学的重要性;通过对平行线性质的推导过程,培养学生的说理能力和思维能力。【教学重点】平行线的性质及运用。【教学难点】性质2和性质3的推理过程。【学情分析】我所在的学校是一农村中学,学生分析推理能力不高,针对所教学生的实际情况,我选取探究、归纳、及讲练结合的教学方法。这节课我让学生通过自己的猜想、动手测量、剪拼,得出平行线的性质1,再由性质1推理性质2、性质3,在教学过程中注重加强训练学生的推理能力,为后继学习证明题的推理过程打下伏笔。【教学内容分析】平行线的性质是证明角相等、研究角的关系的重要依据,是研究几何图形位置关系与数量关系的基础,它不但为三角形内角和定理的证明提供了转化的方法,而且也是今后学习三角形、四边形、平移等知识的学习奠定了理论基础,学好这部分内容至关重要。为了与学生思维发展水平相适应,性质1是通过操作确认的方式得出的,在性质1的基础上经过进一步推理,得到性质2和性质3,这一过程体现了由实验几何到论证几何的过渡,渗透了简单推理,体现了数学在培养良好思维能力方面的价值。【教学方法】情景教学法,合作、探究学习,推理论证法【教学准备】学生:需准备白纸、直尺、三角尺、量角器、剪刀等;教师:进行多媒体制作、利用几何画板进行演示制作。【教学过程】教学环节教学内容设计意图师生活动(一)创设情景导入意大利的比萨斜塔600多年来“斜而不倒”。300多年前物理学家伽利略在塔上做了著名的自由落体实验,使其更加充满了神奇的魅力。目前,它与地面所成的较小的角为85º,若不通过测量的方法,你能知道它与地面所成的较大的角是多少度吗?创设情景,让学生感受到数学来源于生活,从而激发学生探索知识的兴趣与热情。约1.5分钟(二)梳理旧知,引出新课问题1:(1)、在学习新课前,请同学们回忆一下,上节课我们学习了三种平行线的判定方法,分别是什么?(2)、它们的条件和结论分别是什么?(3)、反过来,在两条直线平行的条件下,同位角、内错角、同旁内角又分别有怎样的关系呢?通过复习平行线的判定引入新课,为类比研究平行线判定的过程来构建平行线性质的研究过程作铺垫。学生代表回答(1)、(2),教师点评。(约1.5分钟)(三)动手操作,归纳性质1问题2:两条平行线被第三条直线所截得的同位角会具有怎样的数量关系呢?让学生先指出上图两条平行线被第三条直线所截条件下形成的8个角中,哪些是同位角?并猜想这些同位角的关系,然后让学生利用手中的工具验证自己的猜想。学生演示验证过程后,教师追问:“如果改变截线的位置,那角的度数呢?那同位角相等的关系呢?变还是不变?”学生通过观察老师用几何画板的演示过程,加深对两直线平行的条件下,同位角的关系。总结归纳出平行线的性质1:两直线平行,同位角相等。如上图几何表述为: a∥b∴∠1=∠2让学生经历动手操作——验证猜想——小组交流的探究过程,并且在这一过程中,锻炼学生由图形语言转化为文字语言,再由文字语言转化为数学几何语言的归纳能力和表述能力。学生先对结论进行猜想,然后在老师的引导下独立探究,小组交流,学生代表上台演示,验证猜想结论。如出现操作或表达不规范的地方老师给予指正。学生可能想到的方法:①度量法,用量角器进行测量;②叠合法,通过剪纸、拼图进行比较。(约10分钟)12346578cb21acba21cba21(四)课堂探究,推理验证学习平行线的判定时,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”和“同旁内角互补,两直线平行”你能由性质1,推出两条平行线被第三条直线所截得到的内错角及同旁内角之间的关系吗?请同学们带着这个问题与老师一起进行以下的两个探究活动。探究一:如图:已知a//b,那么∠1与∠2有什...