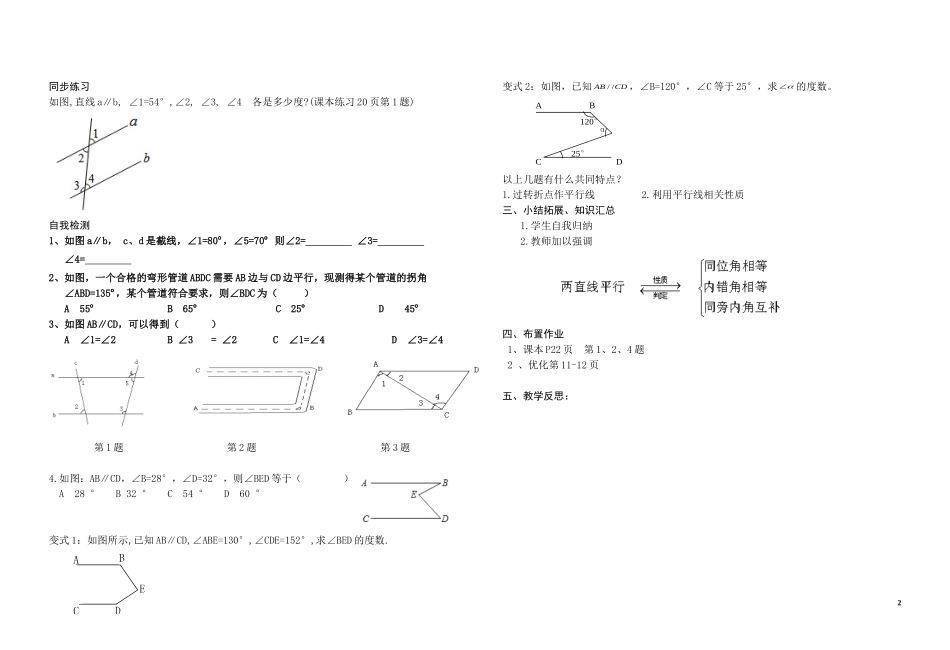
数学公开课教案时间:2017年2月21日地点:七年级(9)班开课人:许凡课题:人教版七年级下册5.3.1《平行线的性质》课型:新授课教学目标:1、理解平行线的性质,掌握他们的图形语言、文字语言、符号语言,并灵活的进行实际应用2、经历观察、实验、猜想、验证等数学活动,培养他们分析问题和解决问题的能力。3、体会几何知识来源于实践并反作用于实践,认识事物的规律是从特殊到一般,再从一般到特殊等辩证唯物主义观点。教学重点:理解并应用平行线的性质。教学难点:探究平行线的性质。教具准备:多媒体课件、量角器、直尺,三角板等教学过程:一、探究新知(一)复习回顾(1)∠3=∠B,则∥(2)∠1=∠4,则∥(3)∠2+∠A=180°,则∥(4)GC∥EF,AB∥EF,则∥(二)动手操作、探求新知如果两条直线平行,那么同位角、内错角、同旁内角又各有什么样的关系呢?这是我们这节课要探究的问题。活动内容:课本18页的“探究”部分。如图,直线a与直线b平行。(1)测量同位角∠1和∠5的大小,它们有什么关系?图中还有其他同位角吗?它们的大小有什么关系?(2)图中有几对内错角?它们的大小有什么关系?为什么?(3)图中有几对同旁内角?它们的大小有什么关系?为什么?(4)换另一组平行线试试,你能得到相同的结论吗?这是本节课的主体部分,具体教学时,可把该探究细分成如下几个活动:活动1、先测量角的度数,把结果填入表内.角∠1∠2∠3∠4∠5∠6∠7∠8度数活动2、根据测量所得的结果作出猜想:同位角具有怎样的数量关系?内错角具有怎样的数量关系?同旁内角呢?活动3、验证猜测.另外画一组平行线被第三条直线所截,同样测量并计算各角的度数,检验刚才的猜想是否成立?如果直线a与b不平行,猜想还成立吗?活动4.你能根据性质1,若直线a∥b,你能根据性质1说明∠3=∠5,∠4+∠5=180°吗?【设计意图】帮助学生理解文字语言,符号语言,图形语言之间的转化,为今后进一步的推理打下基础。活动5、归纳平行线的性质性质1:两条平行直线被第三条直线所截,同位角相等。简称为两直线平行,同位角相等.符号语言表示:∵a∥b∴∠2=∠3性质2:两条平行直线被第三条直线所截,内错角相等。简称为两直线平行,内错角相等.符号语言表示:∵a∥b∴∠1=∠2性质3:两条平行直线按被第三条线所截,同旁内角互补。简称为两直线平行,同旁内角互补.符号语言表示:∵a∥b∴∠2+∠4=180°二、应用新知练一练.如图,平行线AB、CD被直线AE所截,∠1=110°则∠2=。理由:。则∠3=。理由:。则∠4=°理由:。则∠5=°理由:。典例示范例1:如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形另外两个角分别是多少度?.154321EDCBAEDCBA同步练习如图,直线a∥b,∠1=54°,∠2,∠3,∠4各是多少度?(课本练习20页第1题)自我检测1、如图a∥b,c、d是截线,∠1=80º,∠5=70º则∠2=∠3=∠4=2、如图,一个合格的弯形管道ABDC需要AB边与CD边平行,现测得某个管道的拐角∠ABD=135º,某个管道符合要求,则∠BDC为()A55ºB65ºC25ºD45º3、如图AB∥CD,可以得到()A∠1=∠2B∠3=∠2C∠1=∠4D∠3=∠4第1题第2题第3题4.如图:AB∥CD,∠B=28°,∠D=32°,则∠BED等于()A28°B32°C54°D60°变式1:如图所示,已知AB∥CD,∠ABE=130°,∠CDE=152°,求∠BED的度数.变式2:如图,已知ABCD//,∠B=120°,∠C等于25°,求的度数。以上几题有什么共同特点?1.过转折点作平行线2.利用平行线相关性质三、小结拓展、知识汇总1.学生自我归纳2.教师加以强调四、布置作业1、课本P22页第1、2、4题2、优化第11-12页五、教学反思:2AB120°α25°CD