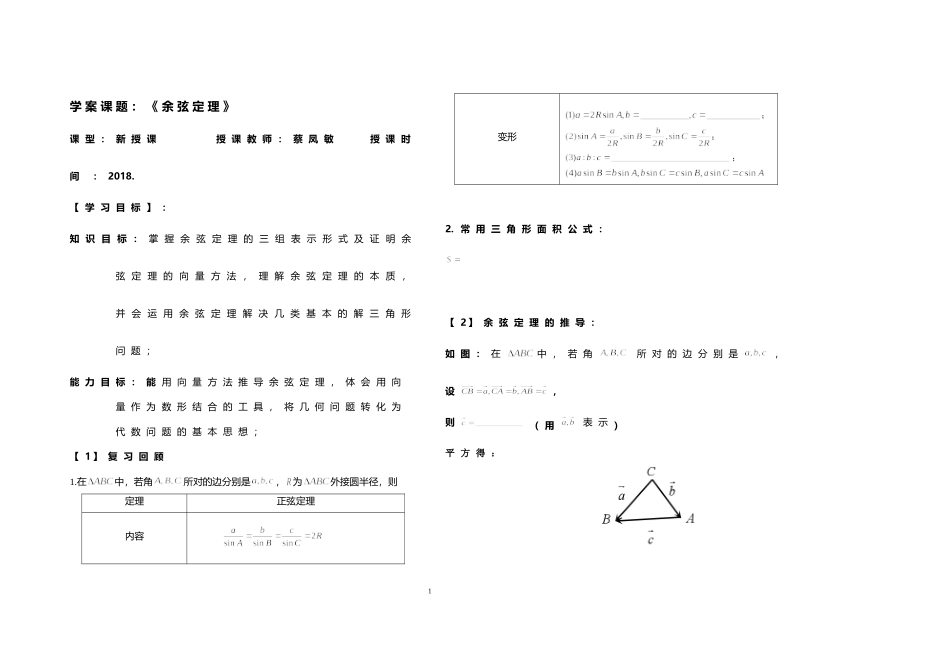
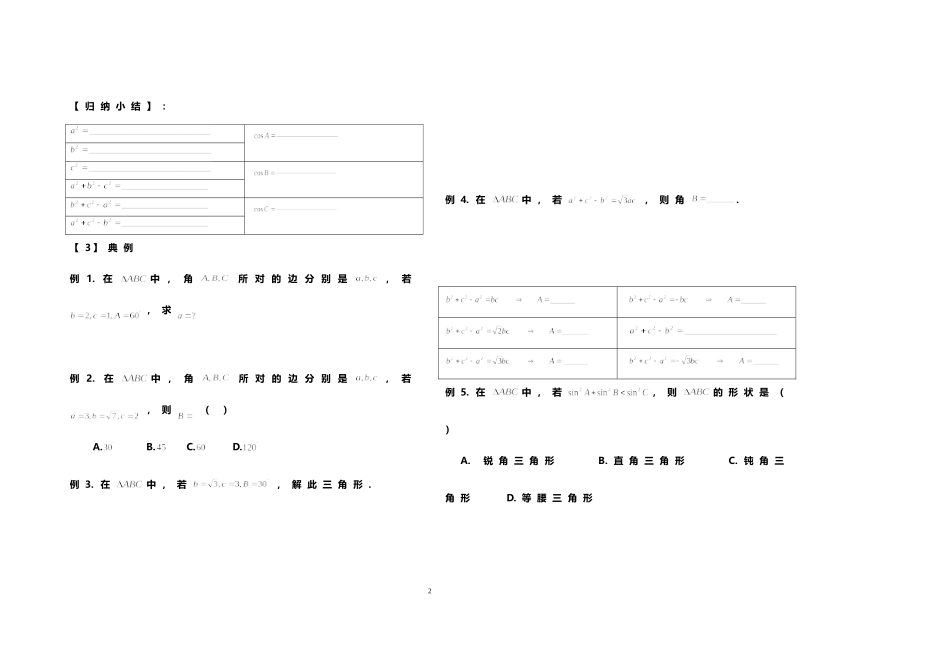
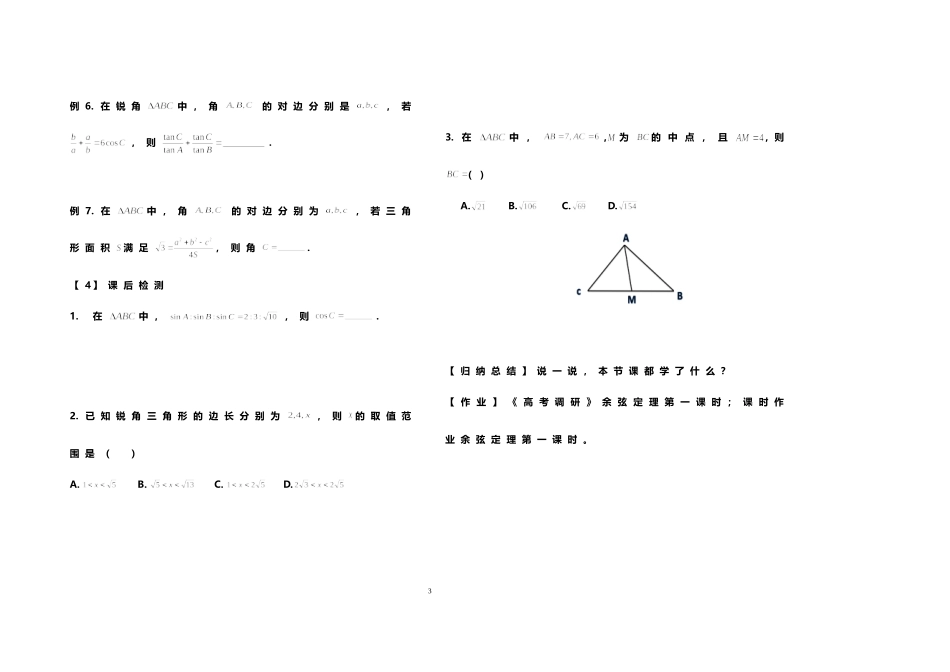
学案课题:《余弦定理》课型:新授课授课教师:蔡凤敏授课时间:2018.【学习目标】:知识目标:掌握余弦定理的三组表示形式及证明余弦定理的向量方法,理解余弦定理的本质,并会运用余弦定理解决几类基本的解三角形问题;能力目标:能用向量方法推导余弦定理,体会用向量作为数形结合的工具,将几何问题转化为代数问题的基本思想;【1】复习回顾1.在中,若角所对的边分别是,为外接圆半径,则定理正弦定理内容变形;;;2.常用三角形面积公式:【2】余弦定理的推导:如图:在中,若角所对的边分别是,设,则(用表示)平方得:1【归纳小结】:【3】典例例1.在中,角所对的边分别是,若,求例2.在中,角所对的边分别是,若,则()A.B.C.D.例3.在中,若,解此三角形.例4.在中,若,则角.例5.在中,若,则的形状是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形2例6.在锐角中,角的对边分别是,若,则.例7.在中,角的对边分别为,若三角形面积满足,则角.【4】课后检测1.在中,,则.2.已知锐角三角形的边长分别为,则的取值范围是()A.B.C.D.3.在中,,为的中点,且,则()A.B.C.D.【归纳总结】说一说,本节课都学了什么?【作业】《高考调研》余弦定理第一课时;课时作业余弦定理第一课时。3