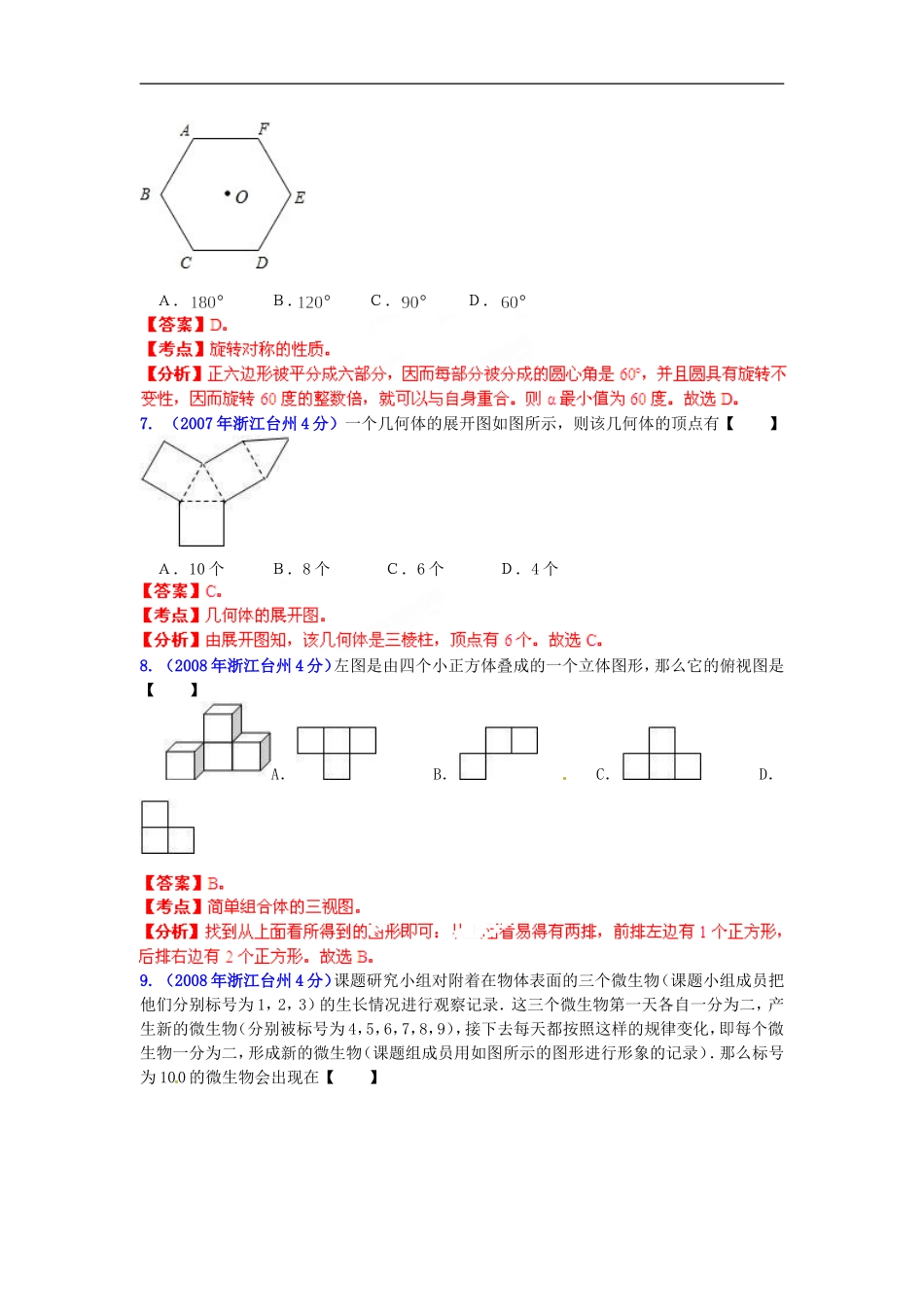
【中考12年】浙江省台州市2001-2012年中考数学试题分类解析专题4图形的变换一、选择题1.(2001年浙江舟山、嘉兴、台州、丽水4分)一个滑轮起重装置如图所示,滑轮半径是10cm,当重物上升10cm时,滑轮的一条半径OA绕轴心O,绕逆时针方向旋转的角度约为(假设绳索与滑轮之间没有滑动,π取3.14,结果精确到1°)【】A.115°B.160°C.57°D.29°2.(2002年浙江台州4分)一个圆锥的底面半径长为4cm,母线长为5cm,则圆锥的侧面积为【】(A)20cm2(B)40cm2(C)20πcm2(D)40πcm23.(2003年浙江台州4分)若圆锥的底面半径为3㎝,母线长为5㎝,则圆锥的侧面积是【】A、15㎝2B、30㎝2C、㎝2D、㎝24.(2004年浙江温州、台州4分)如图,点B在圆锥母线VA上,且VB=VA,过点B作平行与底面的平面截得一个小圆锥的侧面积为S1,原圆锥的侧面积为S,则下列判断中正确的是【】(A)(B)(C)(D)5.(2007年浙江台州4分)下图几何体的主视图是【】A.B.C.D.6.(2007年浙江台州4分)如图,若正六边形ABCDEF绕着中心O旋转角得到的图形与原来的图形重合,则最小值为【】A.B.C.D.7.(2007年浙江台州4分)一个几何体的展开图如图所示,则该几何体的顶点有【】A.10个B.8个C.6个D.4个8.(2008年浙江台州4分)左图是由四个小正方体叠成的一个立体图形,那么它的俯视图是【】A.B.C.D.9.(2008年浙江台州4分)课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为100的微生物会出现在【】A.第3天B.第4天C.第5天D.第6天10.(2009年浙江台州4分)如图,由三个相同小正方体组成的立体图形的主视图是【】A.B.C.D.11.(2010年浙江台州4分)下列立体图形中,侧面展开图是扇形的是【】A.B.C.D.12.(2011年浙江台州4分)下列四个几何体中,主视图是三角形的是【】A.B.C.D.13.(2012年浙江台州4分)如图是一个由3个相同的正方体组成的立体图形,则它的主视图为【】A.B.C.D.二、填空题1.(2004年浙江温州、台州5分)把一个边长为2㎝的立方体截成八个边长为1㎝的小立方体,至少需截▲次。2.(2004年浙江温州、台州5分)已知矩形ABCD的长AB=4,宽AD=3,按如图放置在直线AP上,然后不滑动地转动,当它转动一周时(A→A′),顶点A所经过的路线长等于▲。3.(2005年浙江台州5分)如图,D、E为△ABC两边AB、AC的中点,将△ABC沿线段DE折叠,使点A落在点F处,若∠B=55°,则∠BDF=▲°.4.(2007年浙江台州5分)(1)善于思考的小迪发现:半径为,圆心在原点的圆(如图1),如果固定直径AB,把圆内的所有与轴平行的弦都压缩到原来的倍,就得到一种新的图形椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为▲.(2)(本小题为选做题,做对另加3分,但全卷满分不超过150分)小迪把图2的椭圆绕轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为的球的体积为,则此椭球的体积为▲.5.(2008年浙江台州5分)善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径AB⊥弦CD于E),设AE=x,BE=y,他用含x,y的式子表示图中的弦CD的长度,通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式▲.6.(2009年浙江台州5分)如图,三角板ABC中,∠ACB=90°,∠B=30°,BC=6.三角板绕直角顶点C逆时针旋转,当点A的对应点A'落在AB边的起始位置上时即停止转动,则点B转过的路径长为▲(结果保留π).7.(2010年浙江台州5分)如图,菱形ABCD中,AB=2,∠C=60°,菱形ABCD在...