正弦函数、余弦函数的图像图像1VIP免费

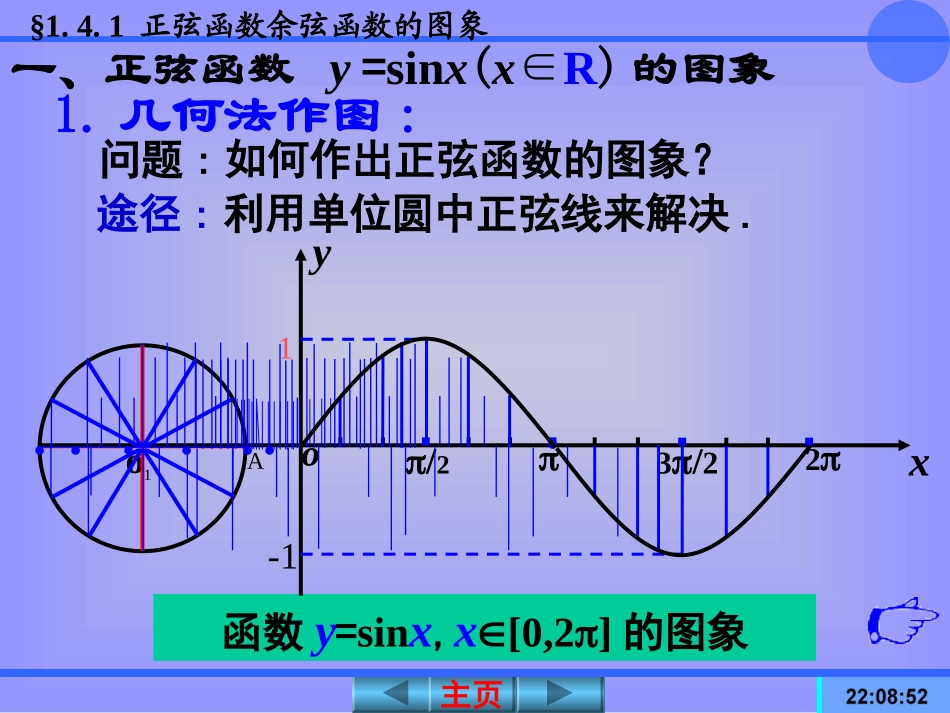
正弦函数、余弦函数的图象主页主页§1.4.1正弦函数余弦函数的图象1.正弦线、余弦线的概念设任意角α的终边与单位圆交于点P.过点P做x轴的垂线,垂足为M.xyoα的终边P(x,y)M则有向线段MP叫做角α的正弦线.有向线段OM叫做角α的余弦线.正弦函数y=sinx与余弦函数y=cosx的定义域都为R主页主页§1.4.1正弦函数余弦函数的图象函数y=sinx,x[0,2]的图象1.几何法作图:一、正弦函数y=sinx(x∈R)的图象问题:如何作出正弦函数的图象？途径:利用单位圆中正弦线来解决.3/2/2o2xyo1A.......1-1主页主页§1.4.1正弦函数余弦函数的图象1-1O3223474yx●●●y=sinx(x∈[0,2π])346●●●●●●●●●●1.几何法作图:63562432761165323主页主页§1.4.1正弦函数余弦函数的图象yxo23423411思考:如何画函数y=sinx(x∈R)的图象?y=sinxx[0,2]y=sinxxRsin(x+2k)=sinx,kZ正弦函数y=sinx,xR的图象叫正弦曲线.主页主页§1.4.1正弦函数余弦函数的图象(1)列表(2)描点(3)连线2,0,sinxxy2.用描点法作图(在精确度要求不太高时)？6323265673423356112xsinx087.01187.05.050.087.087.05.05.023xyO2112000主页主页§1.4.1正弦函数余弦函数的图象3.五点法作图xoy1-12232xoyxoy1-12232☞简图作法(五点作图法)①列表(列出对图象形状起关键作用的五点坐标)②描点(定出五个关键点)③连线(用光滑的曲线顺次连结五个点)☞五个关键点:与x轴的交点(0,0),(,0),(2,0)图像的最高点(,1),2图像的最低点3(,1).2主页主页§1.4.1正弦函数余弦函数的图象xoy3.五点法作图1-1xsinx2301-100022(1)列表(2)描点(3)连线2232主页主页§1.4.1正弦函数余弦函数的图象思考1：观察函数y=x2与y=(x＋1)2的图象，你能发现这两个函数的图象有什么内在联系吗？xyo-1主页主页§1.4.1正弦函数余弦函数的图象思考2：一般地，函数y=f(x＋a)(a>0)的图象是由函数y=f(x)的图象经过怎样的变换而得到的？向左平移a个单位.思考3：设想由正弦函数的图象作出余弦函数的图象，那么先要将余弦函数y=cosx转化为正弦函数，你可以根据哪个公式完成这个转化？主页主页§1.4.1正弦函数余弦函数的图象sinc(os)2xyx二、余弦函数y=cosx(x∈R)的图象(1)图象变换法322x1-1yo342527292(2)五点作图法主页主页§1.4.1正弦函数余弦函数的图象22321-1xyo余弦函数的“五点画图法”五点法的规律是：横轴五点排均匀，上下顶点圆滑行；上凸下凹形相似，游走酷似波浪行.xcosx2322001-101主页主页§1.4.1正弦函数余弦函数的图象2232xyo例1.作函数y=1+sinx,x∈[0,2π]的简图解:列表用五点法描点做出简图xsinxsinx+12322010-10012110主页主页§1.4.1正弦函数余弦函数的图象y=1+sinx,x∈[0,2π]函数y=1+sinx,x∈[0,2π]与函数y=sinx,x∈[0,2π]的图象之间有何联系？例2.作函数y=-cosx,x[0,∈2π]的简图.2232xyo主页主页§1.4.1正弦函数余弦函数的图象解:(1)按五个关键点列表(2)用五点法做出简图函数y=-cosx,与函数y=cosx,x∈[0,2π]的图象有何联系？x0π/2π3π/22πcosx-cosx1-101-1-100102Ox1-1y主页主页§1.4.1正弦函数余弦函数的图象xoyx1-cosx3022201210例3.作函数y=1-cosx,x[0,∈2π]的简图.主页主页§1.4.1正弦函数余弦函数的图象oyx例4.作函数y=|sinx|,x∈R的简图主页主页§1.4.1正弦函数余弦函数的图象oyx?lgsin.1的解有几个方程xx主页主页§1.4.1正弦函数余弦函数的图象练习：（1）作函数y=1+3cosx，x[0,2π]∈的简图(２)作函数y=2sinx-1，x[0,2π]∈的简图（1）yx主页主页§1.4.1正弦函数余弦函数的图象(3)当x∈[0，2π]时，求不等式的解集.1cos2x³5[0,][,2]33pppUxyO2ππ122-112y=主页主页§1.4.1正弦函数余弦函数的图象图象描点法几何法五点法正弦曲线、余弦曲线图象画法主页主页§1.4.1正弦函数余弦函数的图象1.正、余弦函数的图象每相隔2π个单位重复出现，因此，只要记住它们在[0，2π]内的图象形态，就可以画出正弦曲线和余弦曲线.2.作与正、余弦函数有关的函数图象，是解题的基本要求，用“五点法”作图是常用的方法.3.正、余弦函数的图象不仅是进一步研究函数性质的基础，也是解决有关三角函数问题的工具，这是一种数形结合的数学思想.课堂小结课堂小结主页主页§1.4.1正弦函数余弦函数的图象作业：P34第1题P46第1题