定积分在几何中的应用VIP免费

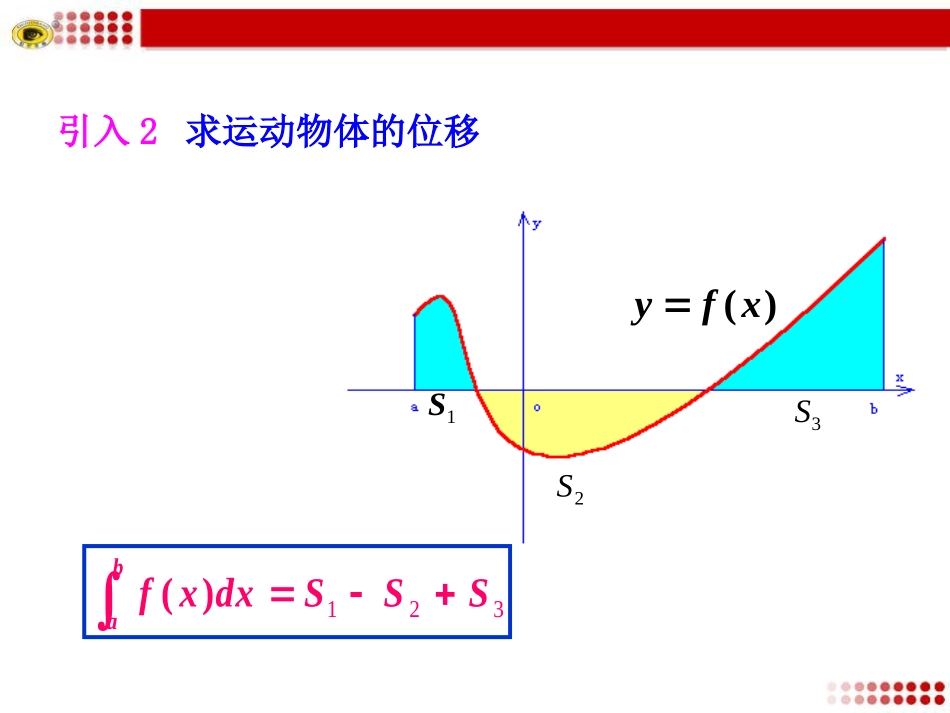
1.7定积分的简单应用1.7.1定积分在几何中的应用badxxfA)(badxxfxfA)]()([12引入1求平面图形的面积:xyo)(xfyabAxyo)(1xfy)(2xfyabA321SSSdxxfba)(1S2S3S)(xfy引入2求运动物体的位移我们已经看到，定积分可以用来计算平面图形的面积，求运动物体的位移，事实上，定积分有着广泛的应用，下面我们就一起学习定积分的简单应用吧！1.理解定积分的几何意义以及微积分的基本定理.2.初步掌握利用定积分求曲边梯形的几种常见题型及方法.（重点、难点）类型1：求由一条曲线y=f(x)和直线x=a,x=b(ag(x)时，由直线x＝a，x＝b(a≠b)和曲线y＝f(x)，y＝g(x)围成的平面图形的面积S＝.bafxgxdx例1计算由两条抛物线2yx和2yx围成图形的面积S.解:作出y2=x,y=x2的图象如图所示:得交点横坐标为x=0及x=1.因此，所求图形的面积为32311002||33xx211.333oxy2yx2yx2xyyxABCDO11200xdxxdx22yxyx解方程组曲边梯形OABC曲边梯形OABDS=S-S【总结提升】求两曲线围成的平面图形的面积的一般步骤:(1)作出示意图;(弄清相对位置关系)(2)求交点坐标，确定图形范围(积分的上限,下限)(3)写出平面图形的定积分表达式；(4)运用微积分基本定理计算定积分，求出面积.例2计算由曲线2yx，直线4yx以及x轴所围成的图形的面积.y=2x解方程组y=x-4直线y=x-4与x轴交点为(4,0).因此，所求图形的面积为2yx4yx解:作出直线y=x-4,曲线的图象如图所示，所求面积为图中阴影部分面积.2yxS1S2得直线y=x-4与曲线y=2x交点的坐标为8,4.将所求平面图形的面积分割成左右两个部分.2yx4xyS1S2488120442[2(4)]SSSxdxxdxxdx332248820442222140(4).3323xxx本题还有其他解法吗？另解1：将所求平面图形的面积分割成左右两个部分.2yx4xyS1S2488120442[2(4)]SSSxdxxdxxdx88042(4)xdxxdx488044(22)(4)xdxxdxxdx382820422140|(4)|.323xxx24400(4)240.3ySydydy还需要把函数y=x-4变形为x=y+4，函数变形为2yx22yx另解2：将所求平面图形的面积看成位于y轴右边的一个梯形与一个曲边梯形的面积之差，因此取y为积分变量例3求两抛物线y＝8－x2，y＝x2所围成的图形的面积．解析作出曲线y＝8－x2，y＝x2的草图，所求面积为图中阴影部分的面积．解方程组，y＝8－x2y＝x2得交点的横坐标为x1＝－2及x2＝2.因此，所求图形的面积为S＝-22(8－x2)dx－-22x2dx＝(8x－13x3)－13x3＝643.(1)求不分割图形面积的步骤为：画图形；求交点(以确定积分上下限)；用定积分表示再计算．(2)一般原则上函数－下函数作被积函数．【总结提升】1．曲线y＝x3与直线y＝x所围成图形的面积等于()A.－11(x－x3)dxB.－11(x3－x)dxC．201(x－x3)dxD．2－10(x－x3)dxC2．曲线y＝sinx与直线x＝－π2，x＝54π，y＝0所围图形的面积为________．4－223．若两曲线y＝x2与y＝cx3(c＞0)围成的图形的面积是23，则c＝________.124.求抛物线y=x2-1，直线x=2，y=0所围成的图形的面积.yx解：如图，由x2-1=0得到抛物线与x轴的交点坐标是(-1,0)，(1,0).所求面积如图阴影所示：所以：212211(1)(1)Sxdxxdx2133118()().333xxxx5.如图，求曲线y＝x2与直线y＝2x所围图形的面积S.解由方程组y＝2x，y＝x2，可得x1＝0，x2＝2.故所求图形的面积为S＝022xdx－02x2dx＝x220－13x320＝43.1.思想方法:数形结合及转化.2.求两曲线围成的平面图形的面积的一般步骤:(1)作出示意图;(弄清相对位置关系)(2)求交点坐标，确定图形范围；(积分的上限,下限)(3)写出平面图形的定积分表达式；(4)运用微积分基本定理计算定积分，求出面积.不闻不若闻之，闻之不若见之，见之不若知之，知之不若行之，学至于行而止矣.——荀况