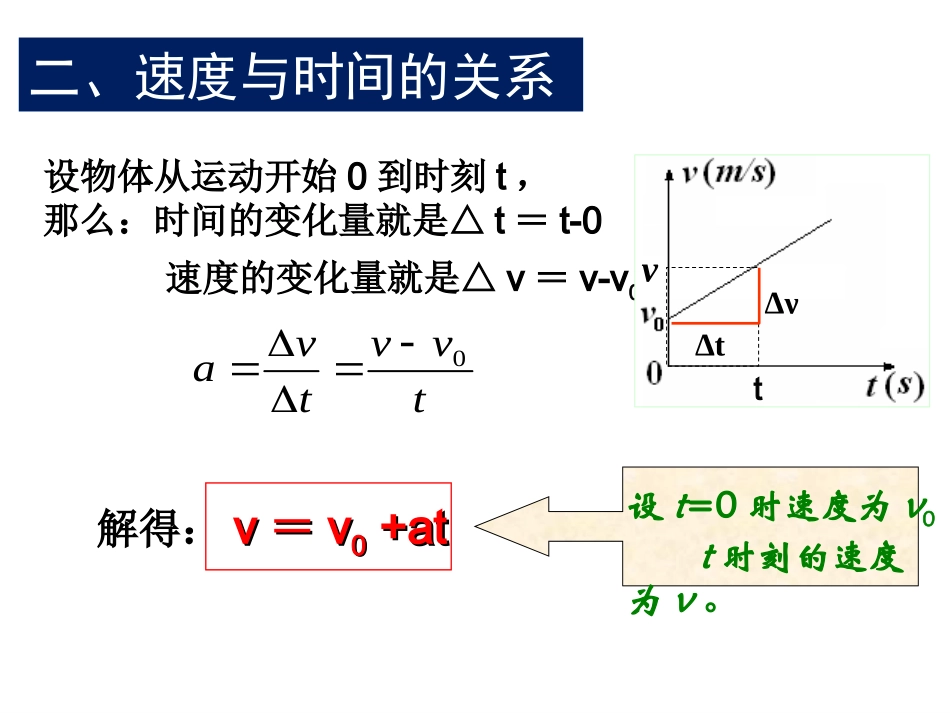
物理定律不能单靠“思维”来获得,还应致力于观察和实验。——普朗克一、匀变速直线运动1.定义:沿着一条直线,且加速度不变的运动。(匀变速直线运动的v-t图象是一条倾斜的直线)2.分类:匀加速直线运动:物体的速度随时间均匀增加。匀减速直线运动:物体的速度随时间均匀减少。vtovto匀加速匀减速例题:课堂讲义例1。设物体从运动开始0到时刻t,那么:时间的变化量就是△t=t-0速度的变化量就是△v=v-v0解得:vv==vv00+at+attvvtva0设t=0时速度为v0t时刻的速度为v。vΔtΔνt二、速度与时间的关系加速度初速度运动过程所用时间末速度vv==vv00++aatt匀变速直线运动公式的说明v=v0+at矢量式注意:在具体运算中必须规定正方向若v0=0则v=at物体做初速度为零的匀加速直线运动若a=0则v=v0物体做匀速直线运动v=v0+at思考思考与讨论与讨论解匀变速直线运动速度与时间关系题目步骤:2、规定正方向(设初速度方向为正方向)。加速运动,a为正值。减速运动,a为负值。3、明确初速度v0、末速度v、加速度a和时间t及各量的正负号。4、将已知量带入公式求未知量,若所求量是矢量,要说明方向。注意:在解题过程中可适当运用图解法。1、画出过程草图。例题1、汽车以40km/h的速度匀速行驶,现以0.6m/s2的加速度加速,10s后速度能达到多少?运动示意图解:以初速度v0=40km/h=11m/s的方向为正方向则10s后的速度:v=v0+at=11+0.6×10m/s=17m/s=62km/h注意:1、公式中的物理量代入具体数值运算时单位要统一2、v0、a、v都是矢量,处理问题时应先选取正方向。(一般选择初速度v0方向为正方向)例题2、某汽车在某路面紧急刹车时,加速度的大小是6m/s2,如果必须在2s内停下来,汽车的行驶速度最高不能超过多少?运动示意图解:以汽车初速度v0方向为正方向则由v=v0+at得v0=v-at=0-(-6)×2m/s=12m/s=43km/h汽车的速度不能超过43km/h三、刹车问题车辆刹车类问题是实际问题,刹车后的车辆可认为是做匀减速直线运动,当速度减小到零时,车辆就会停止,解答此类问题的思路是:先求出它们从刹车到静止的刹车时间t刹,再比较所给时间与刹车时间的关系,确定运动的时间,最后再利用运动学公式求解。注意:对于末速度为零的匀减速直线运动,也可以采用逆向思维法,即把运动倒过来看成是初速度为零的匀加速直线运动。例题3、某汽车正以12m/s的速度在路面上匀速行驶,前方出现紧急情况需刹车,加速度大小是3m/s2,求汽车5s末的速度。解:以初速方向为正方向则v=v0+at=12+(-3)×5m/s=-3m/s正确解法:以初速方向为正方向当车速减为零时,v=v0+at=12-3t=0解得t=4s即4s末汽车已刹车完毕,所以5末时汽车处于静止状态,即速度为零。刹车问题注意:(与实际相符)总结1.匀变速直线运动2.匀变速直线运动的速度公式沿着一条直线,且加速度不变的运动。v=v0+at分类匀加速直线运动匀减速直线运动作业:课后第1、2题