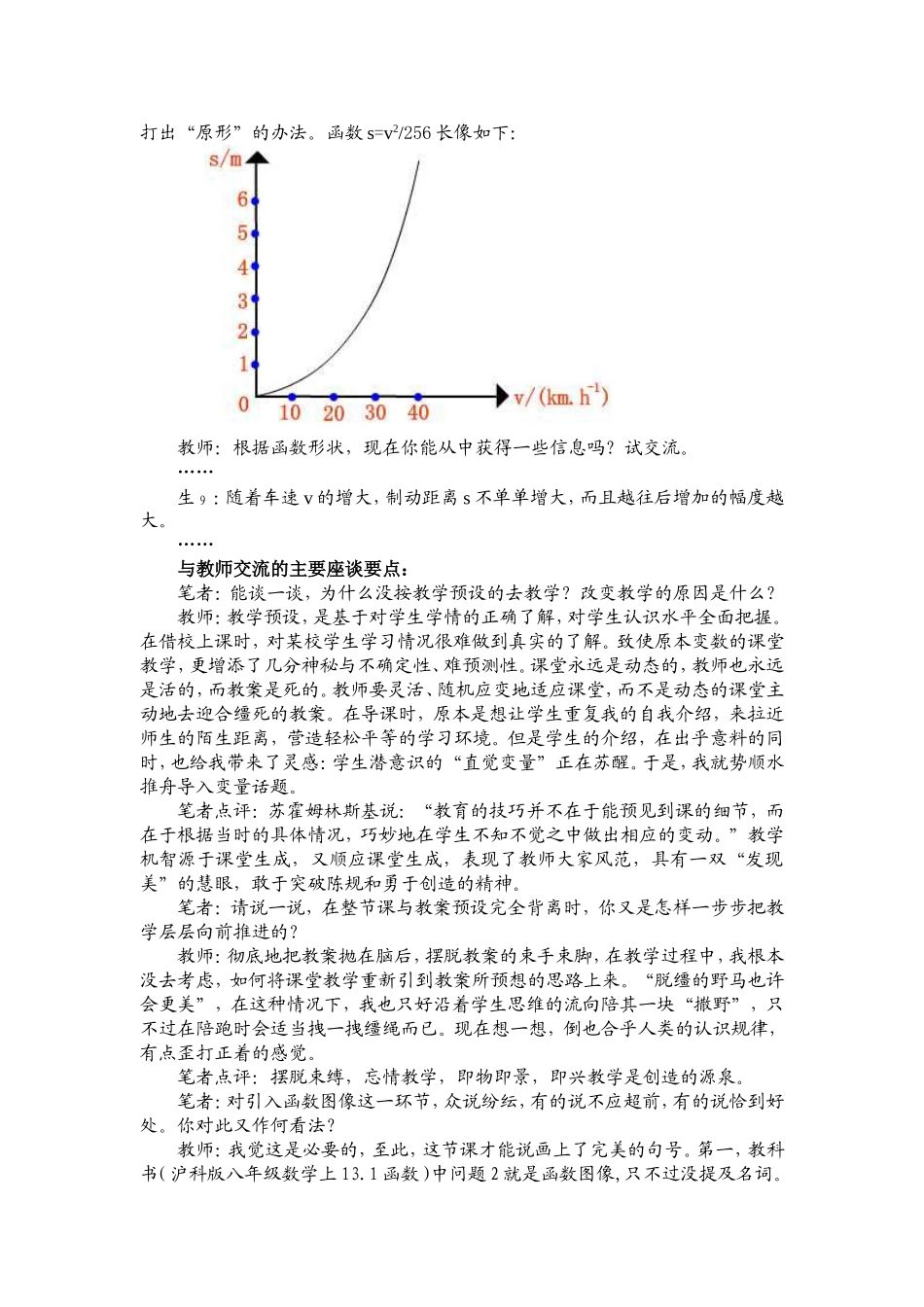
一节还原概念原发性思考过程的函数教学实录与交流、欣赏皖安庆市五横初级中学戴向阳(邮编:246051手机:13225725503身份证:34082219741016051x)皖安庆市怀宁县秀山中学戴向前函数概念的学习,一直是初中生数学学习中的难点,不久前笔者参加了一次“同课异构——函数概念教学研讨会”,听了一节别出心裁的函数新授课。听后笔者只想说:难点不再难。这是一节基于人类认识函数过程的原创史的教学,但又不是简简单单的函数发展史对函数概念的罗列。这是函数概念教学的一次创新——再现了人类对函数概念的原发性思考。在短短的45分钟内,授课教师从实际情景出发,逐级推进,以螺旋上升的方式抽象并提出函数概念。整节课有四个发展阶段,可概括为:①直觉变量;②数值步入变量;③对应引入函数;④数形结合升华函数。无怪乎,听课教师赞誉为“函数概念四部曲”。下面笔者结合教学实录分四个片断,简要摘录如下:片断一:唤醒直觉变量,发现变量的因果关系。教师:同学们好!我来自秀山中学,名叫戴向前,男,33岁,身高170厘米,体重131斤。如果一年后,我们再次相聚时,哪位同学能帮我作一下自我介绍吗?片刻寂静后,生1:我来自秀山中学,名叫戴向前,男,34岁,身高170厘米,体重131斤。生2抢过话茬:我来自秀山中学,名叫戴向前,男,34岁,身高170厘米左右,体重约131斤。教师:两种介绍一样吗?谁的介绍合理些?学生你一言我一语,得出一致结论:姓名、姓别、工作单位,通常不会变,年龄身高、体重会变化。教师:同学们谈得很好,生活中存在两种量,一种量不会改变,另一种量会变化。我们称不会改变的量叫常量,会变化的量叫变量。……学生通过“自我介绍”话题,轻而易举地感受出常量与变量的不同。教师望着校园里整整齐齐的车辆:看来我们同学骑车上学很多,想必多数同学对刹车会有深切的感受。同学能教老师一些刹车经验吗?生3:车速越快,越难刹住,骑车不能快。生4:车速越快,刹车时车子滑行距离越长,易出事故。教师:感谢两位同学的经验,老师骑车以后会注意。请同学们思考一下,刹车过程中有哪些量,它们间有关系吗?有怎样的关系?生2:有两个量,车速和滑行距离。生5:两个都是变量。生6:两个变量,互相影响。生1果断道:不,车速影响到滑行距离,滑行距离不影响车速。话音刚落,全场投以赞许的目光。教师:与刹车类似,生活中还有许多过程,它们或多或少都包罗着一定的变量,请同学们再举一些含有两个变量的例子,思考两个变量是否有因果联系?哪个是因,哪个是果?(同学们畅所欲言,气氛热烈,师生互动,共同完成了自变量与因变量的学习,内容略)片断二:数值步入变量,由定性认识过渡到定量认识。教师:前面刚认识了,车速越快,刹车距离越长。车速改变,刹车距离也跟着改变。根据经验,刹车时,车速总有一个数值,车速这个变量是可以量化的。刹车距离是否也可以量化呢?接看下面问题:【问题】车辆行驶过程中,由于惯性的作用制动后仍滑行一段距离才能停住。某型号的车辆在路面上的制动距离sm与车速vkm/h之间有下列经验公式:s=v2/256。请填补下表:车速v01020304050…制动距离s学生借助计算器,合作填表如下:车速v01020304050…制动距离s00.41.63.56.39.8…教师:生活中多数变量是可以量化的。如问题中车速v和制动距离s,我们数学关注的是生活中可以量化的“直觉变量”。象刚才有的同学说的:人的品质会随社会阅历而改变,人会因为时间变老而毛发越来越秃。这些变化因无法量化,在数学上通常不谈。数学关注的是“数值”变量。同学们还能举出一些身边的“数值”变量吗?片断三:对应引入函数教师:从问题的表格中可以看出,当速度v每给一值时,制动距离s就会相应得到一个值。反之,如果给制动距离s一个值时,速度v如何呢?你是怎么思考的约三分钟后,生6:当s取4时,算得v有两个值±32。生7:给s取9,算出v也有两个值±48,不过-48不符合实际舍去。生8:对,v=±256s,s每给一值,v会有两个值,其中负的应舍去。可以说,给制动距离s一个值,速度v会得到唯一的一个值。教师:如果不考虑实际,单纯就式子v=±256s本身来看呢?生齐答:制动距离s每取一个值,速度v...