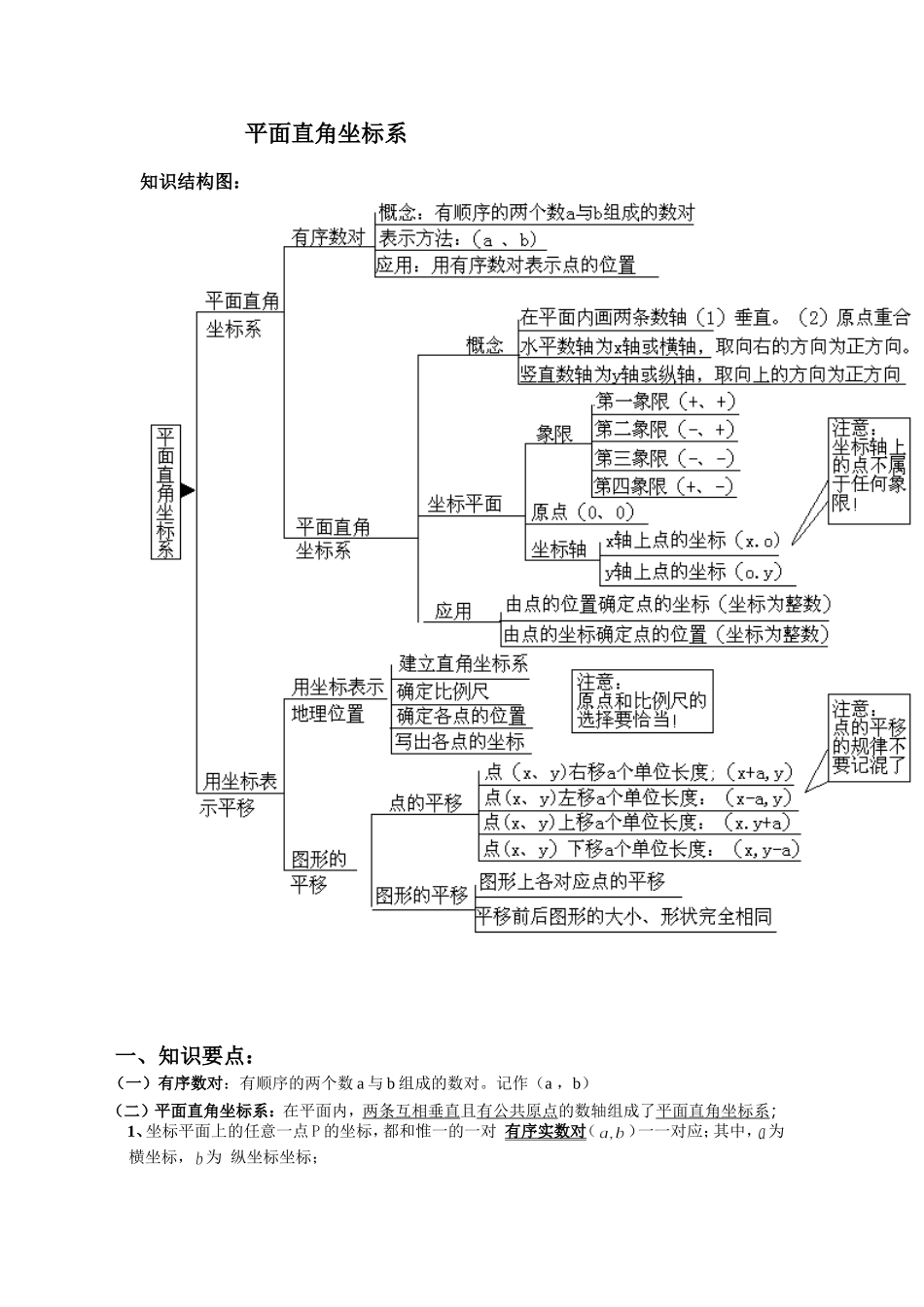
平面直角坐标系知识结构图:一、知识要点:(一)有序数对:有顺序的两个数a与b组成的数对。记作(a,b)(二)平面直角坐标系:在平面内,两条互相垂直且有公共原点的数轴组成了平面直角坐标系;1、坐标平面上的任意一点P的坐标,都和惟一的一对有序实数对()一一对应;其中,为横坐标,为纵坐标坐标;2、轴上的点,纵坐标等于0;轴上的点,横坐标等于0;坐标轴上的点不属于任何象限(三)四个象限的点的坐标具有如下特征:1、点P()所在的象限横、纵坐标、的取值的正负性;2、点P()所在的数轴横、纵坐标、中必有一数为零;(四)在平面直角坐标系中,已知点P,则1、点P到轴的距离为;2、点P到轴的距离为;3、点P到原点O的距离为PO=(五)平行直线上的点的坐标特征:1、在与轴平行的直线上,所有点的纵坐标相等;点A、B的纵坐标都等于;2、2、在与轴平行的直线上,所有点的横坐标相等;点C、D的横坐标都等于;(六)对称点的坐标特征:1、点P关于轴的对称点为,即横坐标不变,纵坐标互为相反数;2、点P关于轴的对称点为,即纵坐标不变,横坐标互为相反数;象限横坐标纵坐标第一象限正正第二象限负正第三象限负负第四象限正负P()abxyOXYABBXYCD3、点P关于原点的对称点为,即横、纵坐标都互为相反数;关于x轴对称关于y轴对称关于原点对称(七)两条坐标轴夹角平分线上的点的坐标的特征:1、若点P()在第一、三象限的角平分线上,则,即横、纵坐标相等;2、若点P()在第二、四象限的角平分线上,则,即横、纵坐标互为相反数;在第一、三象限的角平分线上在第二、四象限的角平分线上(八)利用平面直角坐标系绘制区域内一些点分布情况平面图过程如下:1、建立坐标系,选择一个适当的参照点为原点,确定x轴、y轴的正方向;2、根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;3、在坐标平面内画出这些点,写出各点的坐标和各个地点的名称。(九)用坐标表示平移:见下图二、题型分析:题型一:代数式与点坐标象限判定此类问题通常与不等式(组)联系在一起,或由点所在的象限确定字母的取值范围,或由字XyP1PnnmOXyP2PmmnOXyP3PmmnOnXyPmnOyPmnOXP(x,y)P(x,y-a)P(x-a,y)P(x+a,y)P(x,y+a)向上平移a个单位长度向下平移a个单位长度向右平移a个单位长度向左平移a个单位长度母的取值范围确定点所在的象限.【例1】在平面直角坐标系中,点在()A.第一象限B.第二象限C.第三象限D.第四象限【解析】由各象限点的特征知,点在第四象限,故选D.【点评】解答这类问题所需的知识点是第一、二、三、四象限内的点的坐标符号分别是(+,+)、(-,+)、(-,-)、(-,+).【例2】若点()的横坐标与纵坐标互为相反数,则点一定在()A.第一象限B.第二象限C.第三象限D.第四象限【解析】由题意知,解得于是点P的坐标为(1,-1),于是点P在第二象限.选B.【点评】本题设置了一个小小的障碍,即先根据横坐标与纵坐标互为相反数列出方程解出m,然后才能根据会标特点确定象限.【例3】若点P(a,b)在第四象限,则点M(b-a,a-b)在()A、第一象限B、第二象限C、第三象限D、第四象限答案:B分析:第四象限横坐标大于0,纵坐标小于0.【例4】如果a-b<0,且ab<0,那么点(a,b)在()A、第一象限B、第二象限C、第三象限,D、第四象限.答案:B【例5】对任意实数x,点P(x,x2-2x)一定不在()A.第一象限B.第二象限C.第三象限D.第四象限答案:C【例7】点P(x,y)在第四象限,且|x|=3,|y|=2,则P点的坐标是。答案:(3,-2)【例8】若点M(1–x,x+2)在第二象限内,则x的取值范围为;答案:x>2习题演练:1、在平面直角坐标系中,点P()一定在象限。2、点P(x-1,x+1)不可能在()A、第一象限B、第二象限C、第三象限D、第四象限3、如果点M(a+b,ab)在第二象限,那么点N(a,b)在第________象限。4、点Q(3–a,5–a)在第二象限,则=;5、点M(a,a-1)不可能在()A、第一象限B、第二象限C、第三象限D、第四象限6、如果xy<0,那么点P(x,y)在()A、第二象限B、第四象限C、第四象限或第二象限D、第一象限或第三象限题型二:用代数式求...