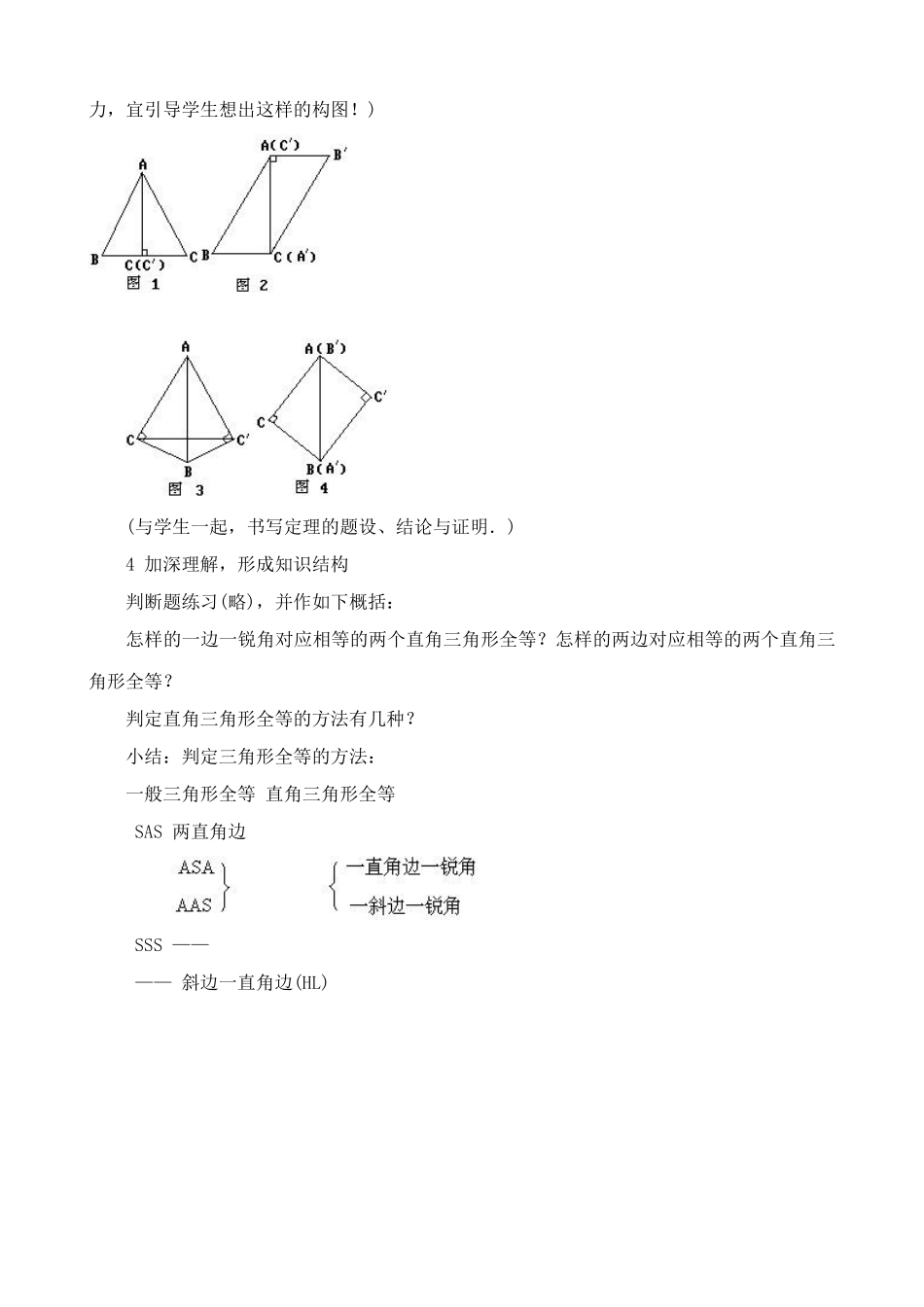
直角三角形全等的判定[主持人按:彭加勒说过“数学的真理是用一连串无懈可击的推理,从少数一目了然的命题推演出来的”.数学家们的喜好是要把这样的推演和谐地一直扩展到极致,数学史反映的发展历程可以为证.和谐扩展也是数学学科知识展开的主要方式与准则,常见的有三种类型:由特殊扩展到一般;由一般引出特殊;类似情况扩展.和谐性表现在主要公式法则形式上的不变性;内在的无矛盾性;安排展开的相似性.这为教学与学习也带来了极大的方便.然而,既然是扩展,总不是完全一样的,总会有一些相异的性质.忽视(即使是无意的)这一面,必然也会带来负面的影响.“利用和谐性,揭示相异处”,是教师在处理这类课题时的座右铭.本期的两篇设计,正是关于两类扩展的课题.]1从一般到特殊T:我们已学过一般三角形全等的判定.请大家以此为依据,诊断一下:(1)有两角和一边对应相等的两个三角形全等.()(2)有两边及其夹角对应相等的两个三角形全等.()(3)有两边和其中一边的对角对应相等的两个三角形全等.()如果不一定全等,请举出反例.请说明判定一般三角形全等的依据的共同点(要有三组对应元素相等).那么,如何判定直角三角形的全等呢?直角三角形是一般三角形的特殊情形,一般三角形全等的判定定理自然也适用于直角三角形的全等的判定.特殊情形往往也有它自身的特殊的性质[评:一般素质的熏陶语言],直角三角形全等也有它自身独特的判定定理么?这就是本节课的课题.2枚举情况,发现命题T:判定一般三角形全等,要有三组对应元素相等;两个直角三角形,已有直角相等的条件,一般还需要几对元素对应相等呢?S:两对.T:怎样的两对呢,我们一起来探索一下.(1)两角.显然不行.(2)一边一角,又可分为:直角边与一锐角;斜边与一锐角,这已包含在一般的两角一边中了.(3)两边.可分为:两直角边;一直角边与一斜边.前者已包在一般的两边一夹角中了.剩下的只要探讨:斜边与一直角边对应相等的两个直角三角形全等么?[评:这样的枚举情况,探索发现的过程,容易操作,恰是很好的素质培养的手段.]T:请同学们在纸上画图:(1)画一个斜边长为5cm,直角边长为3cm的直角三角形;(2)画△ABC,使AB=5cm,AC=3cm,∠B=30°.你们有什么发现没有?(叠合比较后发现:(1)中的直角三角形都是全等的;(2)中的一般三角形有两个不同的图形)实验探索,引导我们提出了一个猜想:有斜边和一直角边对应相等的两个直角三角形全等.3借助一般,探索证明T:怎样来证明这个命题?明确地问:应借助什么定理来证明这个命题?S:一般三角形全等的判定定理.T:据此,只要去证明什么?S1:另一直角边对应相等.S2:一个锐角对应相等.T:明确了方向[评:这是每一个重要的证明前,最需要做好的工作!]后,剩下的才是考虑:如何去完成它?教师启发学生如下的两条途径:(1)借助勾股定理,先证明第三边也相等;(2)利用拼合已知相等的对应边的办法,具体地说有:拼合直角边(已知相等的边),有两种办法:拼合斜边,也有两种办法(虽然,按图2、图4的证法,如今尚困难.但为了发展想象能力,宜引导学生想出这样的构图!)(与学生一起,书写定理的题设、结论与证明.)4加深理解,形成知识结构判断题练习(略),并作如下概括:怎样的一边一锐角对应相等的两个直角三角形全等?怎样的两边对应相等的两个直角三角形全等?判定直角三角形全等的方法有几种?小结:判定三角形全等的方法:一般三角形全等直角三角形全等SAS两直角边SSS————斜边一直角边(HL)