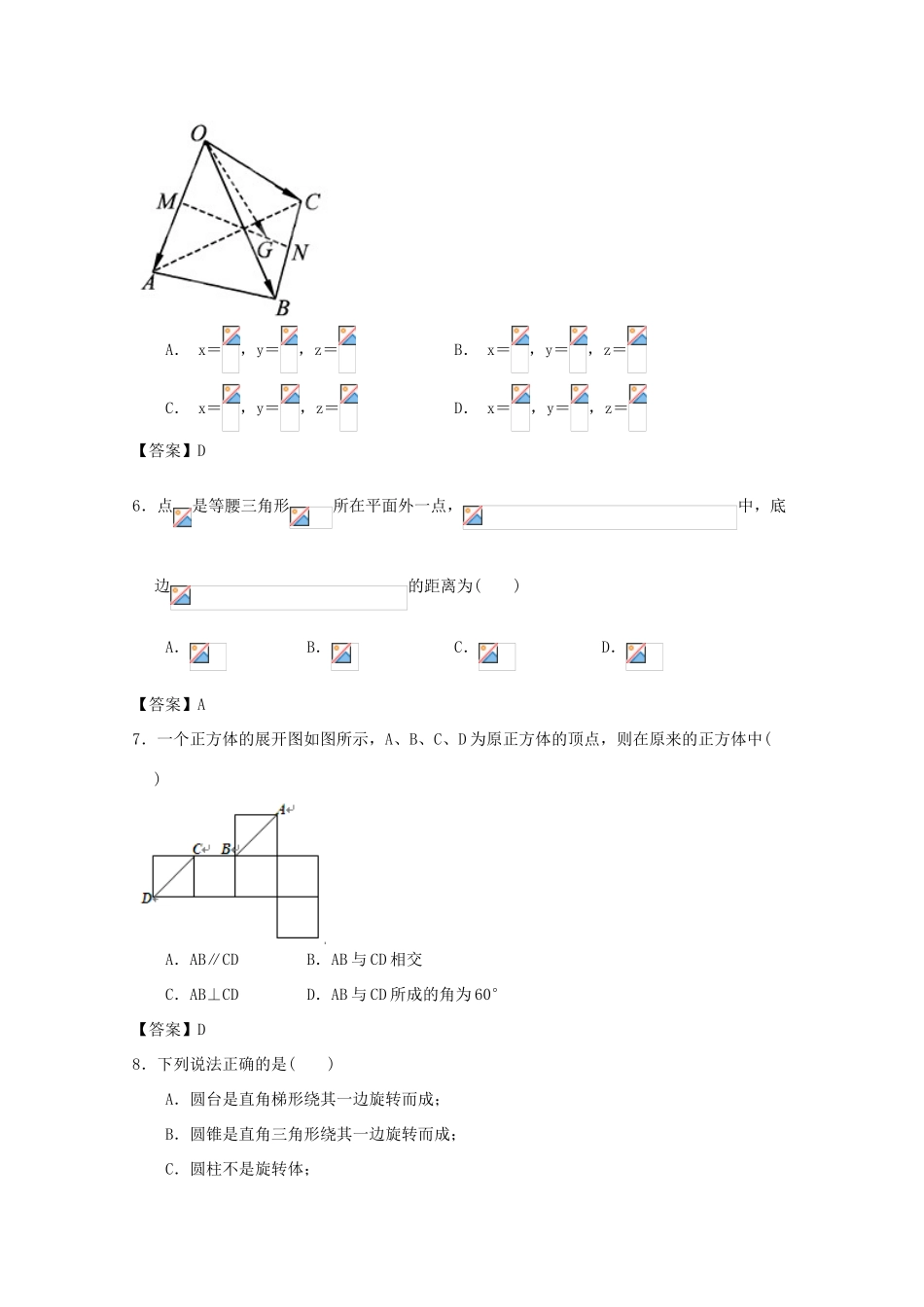
空间几何体一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.正方体中,、、分别是、、的中点.那么,正方体的过、、的截面图形是()A.三角形B.四边形C.五边形D.六边形【答案】A2.在空间直角坐标系中,点P(2,3,4)与Q(2,3,-4)两点的位置关系是()A.关于x轴对称B.关于xOy平面对称C.关于坐标原点对称D.以上都不对【答案】B3.圆台的一个底面周长是另一个底面周长的倍,母线长为,圆台的侧面积为,则圆台较小底面的半径为()A.B.C.D.【答案】A4.如图,是由4个相同小正方体组合而成的几何体,它的左视图是()A.B.C.D.【答案】D5.如图,已知空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且,现用基向量表示向量,设,则x、y、z的值分别是()A.x=,y=,z=B.x=,y=,z=C.x=,y=,z=D.x=,y=,z=【答案】D6.点是等腰三角形所在平面外一点,中,底边的距离为()A.B.C.D.【答案】A7.一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中()A.AB∥CDB.AB与CD相交C.AB⊥CDD.AB与CD所成的角为60°【答案】D8.下列说法正确的是()A.圆台是直角梯形绕其一边旋转而成;B.圆锥是直角三角形绕其一边旋转而成;C.圆柱不是旋转体;D.圆台可以看作是平行底面的平面截一个圆锥而得到【答案】D9.设,是两条不同的直线,是一个平面,则下列命题正确的是()A.若,,则B.若,,则C.若,,则D.若,,则【答案】A10.如图,点P、Q、R、S分别在正方体的四条棱上,并且是所在棱的中点,则直线PQ与RS是异面直线的一个图是()【答案】C11.某几何体的三视图如图所示,则该几何体的体积是()A.B.2C.D.【答案】A12.已知平面α外的直线b垂直于α内的二条直线,有以下结论:b一定不垂直于α;b可能垂直于平面α;b一定不平行于平面α,其中正确的结论有()A.0个B.1个C.2个D.3个【答案】B二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.在空间直角坐标系中,若点点,则.【答案】14.一个几何体的三视图及部分数据如图所示,左视图为等腰三角形,俯视图为正方形,则这个几何体的体积等于.【答案】15.四棱锥的三视图如右图所示,四棱锥的五个顶点都在一个球面上,、分别是棱、的中点,直线被球面所截得的线段长为,则该球表面积为.【答案】16.一个几何体的三视图如下图所示,正视图是一个边长为2的正三角形,侧视图是一个等腰直角三角形,则该几何体的体积为.【答案】4三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.如图,已知平行四边形中,,,,,垂足为,沿直线将翻折成,使得平面平面.连接,是上的点.(I)当时,求证平面;(Ⅱ)当时,求二面角的余弦值.【答案】(1) ,平面平面,∴.如图建立空间直角坐标系.则,,,,,.,,. ,,∴,.又,∴平面.设面的法向量为,则.取,,则,又平面的法向量为,∴.∴二面角的余弦值.18.如图所示,已知M、N分别是AC、AD的中点,BCCD.(I)求证:MN∥平面BCD;(II)求证:平面BCD平面ABC;(III)若AB=1,BC=,求直线AC与平面BCD所成的角.【答案】(1)因为分别是的中点,所以.又平面且平面,所以平面.(2)因为平面,平面,所以.又,所以平面.又平面,所以平面平面.(3)因为平面,所以为直线与平面所成的角.在直角中,,所以.所以.故直线与平面所成的角为.19.如图,已知正三棱柱各棱长都为,为线段上的动点.(Ⅰ)试确定的值,使得;(Ⅱ)若,求二面角的大小;【答案】【法一】(Ⅰ)当时,作在上的射影.连结.则平面,∴,∴是的中点,又,∴也是的中点,即.反之当时,取的中点,连接、. 为正三角形,∴.由于为的中点时, 平面,∴平面,∴.(Ⅱ)当时,作在上的射影.则底面.作在上的射影,连结,则.∴为二面角的平面角.又 ,∴,∴.∴,又 ,∴.∴,∴的大小为.【法二】以为原点,为轴,过点与垂直的直线为轴,为轴,建立空间直角坐标系,如图所示,设,则、、.(Ⅰ)由得,即,∴,即为的中点,也即...