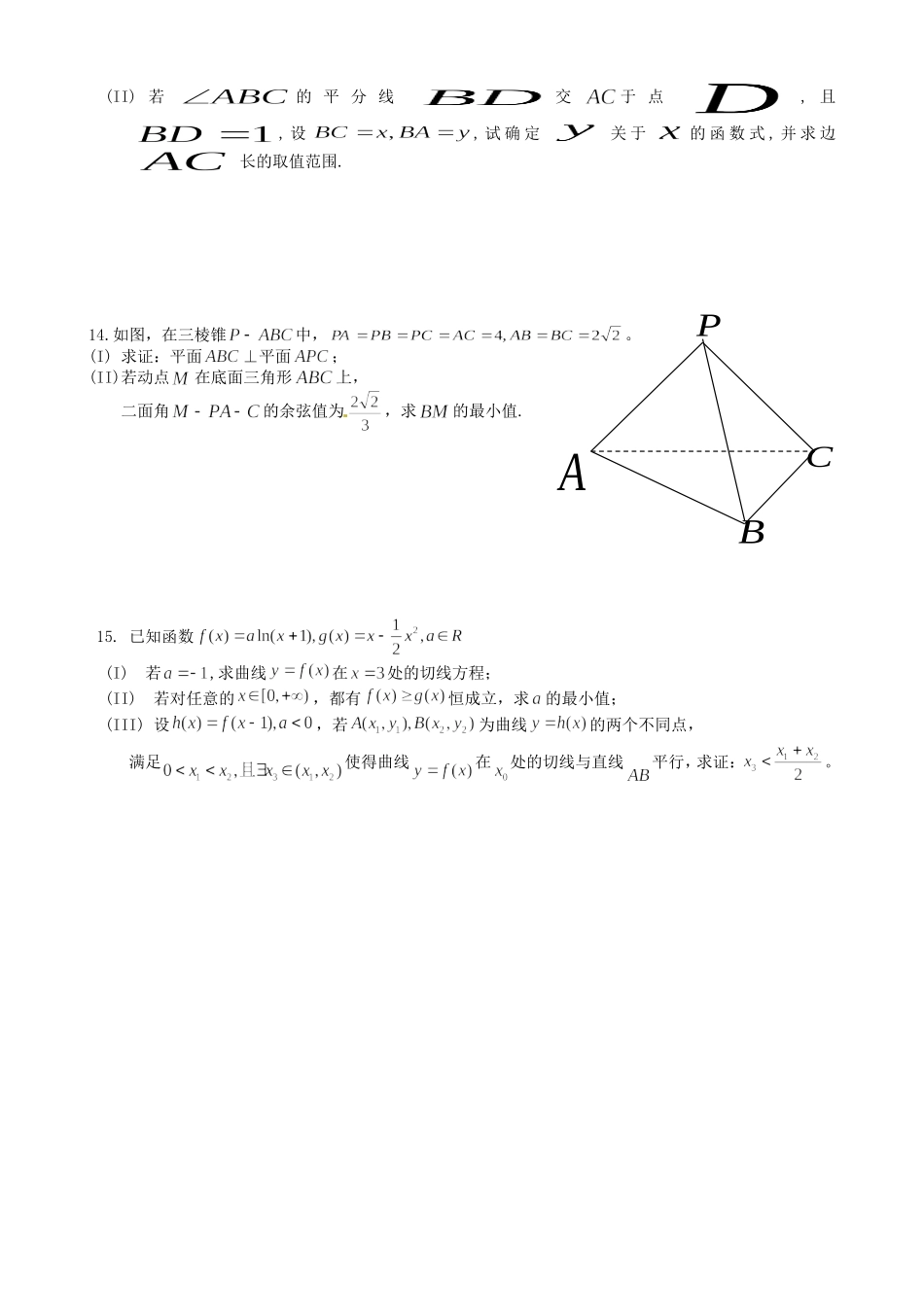
高三第一学期期末综合练习(四)1.设不等式组表示的平面区域为.若圆C:经过区域上的点,则的取值范围是()(A)(B)(C)(D)2.已知各项均不为零的数列,定义向量,则下列命题中是真命题的是()(A)若对任意的,都有∥成立,则数列是等差数列(B)若对任意的,都有∥成立,则数列是等比数列(C)若对任意的,都有⊥成立,则数列是等差数列(D)若对任意的,都有⊥成立,则数列是等比数列3.若关于的方程有三个不相同的实数根,则实数的取值范围是()(A)(B)(C)(D)4.已知双曲线22221(0,0)xyabab,是实轴顶点,是右焦点,是虚轴端点,若在线段上(不含端点)存在不同的两点,使得构成以为斜边的直角三角形,则双曲线离心率e的取值范围是()(A)(B)(C)(D)5.已知正四面体中,为的中点,则过点与侧面和底面所在平面都成的平面共有(注:若二面角的大小为,则平面与平面所成的角也为)()(A)2个(B)4个(C)6个(D)无数个6.已知{an}是首项为1的等比数列,若Sn是{an}的前n项和,且28S3=S6,则数列的前4项和为______.7.经过点P(2,-3)作圆x2+2x+y2=24的弦AB,使得点P平分弦AB,则弦AB所在直线的方程为_______。8.已知点P在曲线y=41xe上,a为曲线在点P处的切线的倾斜角,则a的取值范围是.9.已知和是平面内互相垂直的两条直线,它们的交点为,动点分别在和上,且,则过三点的动圆扫过的区域的面积为.10.已知点为坐标原点,点满足则的最大值是______.11.设为实常数,是定义在R上的奇函数,当时,,若对一切成立,则的取值范围为________.12.记为不超过实数的最大整数,例如,,,.设为正整数,数列满足,,现有下列命题:①当时,数列的前3项依次为5,3,2;②对数列都存在正整数,当时总有;③当时,;④对某个正整数,若,则.其中的真命题有.(写出所有真命题的编号)13.在中,分别为角所对的边,向量,,且垂直.(I)确定角的大小;APCB(II)若的平分线交于点,且,设,试确定关于的函数式,并求边长的取值范围.14.如图,在三棱锥中,。(I)求证:平面⊥平面;(II)若动点在底面三角形上,二面角的余弦值为,求的最小值.15.已知函数(I)若,求曲线在处的切线方程;(II)若对任意的,都有恒成立,求的最小值;(III)设,若为曲线的两个不同点,满足使得曲线在处的切线与直线平行,求证:。答案6.设不等式组表示的平面区域为.若圆C:经过区域上的点,则的取值范围是(B)(A)(B)(C)(D)7.已知各项均不为零的数列,定义向量,则下列命题中是真命题的是(A)(A)若对任意的,都有∥成立,则数列是等差数列(B)若对任意的,都有∥成立,则数列是等比数列(C)若对任意的,都有⊥成立,则数列是等差数列(D)若对任意的,都有⊥成立,则数列是等比数列8.若关于的方程有三个不相同的实数根,则实数的取值范围是(D)(A)(B)(C)(D)9.已知双曲线22221(0,0)xyabab,是实轴顶点,是右焦点,是虚轴端点,若在线段上(不含端点)存在不同的两点,使得构成以为斜边的直角三角形,则双曲线离心率e的取值范围是(D)(A)(B)(C)(D)10.已知正四面体中,为的中点,则过点与侧面和底面所在平面都成的平面共有(B)(注:若二面角的大小为,则平面与平面所成的角也为)(A)2个(B)4个(C)6个(D)无数个11.已知{an}是首项为1的等比数列,若Sn是{an}的前n项和,且28S3=S6,则数列的前4项和为______.12..经过点P(2,-3)作圆x2+2x+y2=24的弦AB,使得点P平分弦AB,则弦AB所在直线的方程为_______。13..已知点P在曲线y=41xe上,a为曲线在点P处的切线的倾斜角,则a的取值范围是_______.14.已知和是平面内互相垂直的两条直线,它们的交点为,动点分别在和上,且,则过三点的动圆扫过的区域的面积为_______.15.已知点为坐标原点,点满足则的最大值是_____________.16.设为实常数,是定义在R上的奇函数,当时,,若对一切成立,则的取值范围为________.17.记为不超过实数的最大整数,例如,,,.设为正整数,数列满足,,现有下列命题:①当时,数列的前3项依次为5,3,2;②对数列都存在正整数,当时总有;③当时,;④对某个正整数,若,则.其中的真命题有_________.(写出所有真命题的编号)11)、;(12)、x-y-5=0;(13)、;(14)、18∏;(15)、;(16)、;(17...