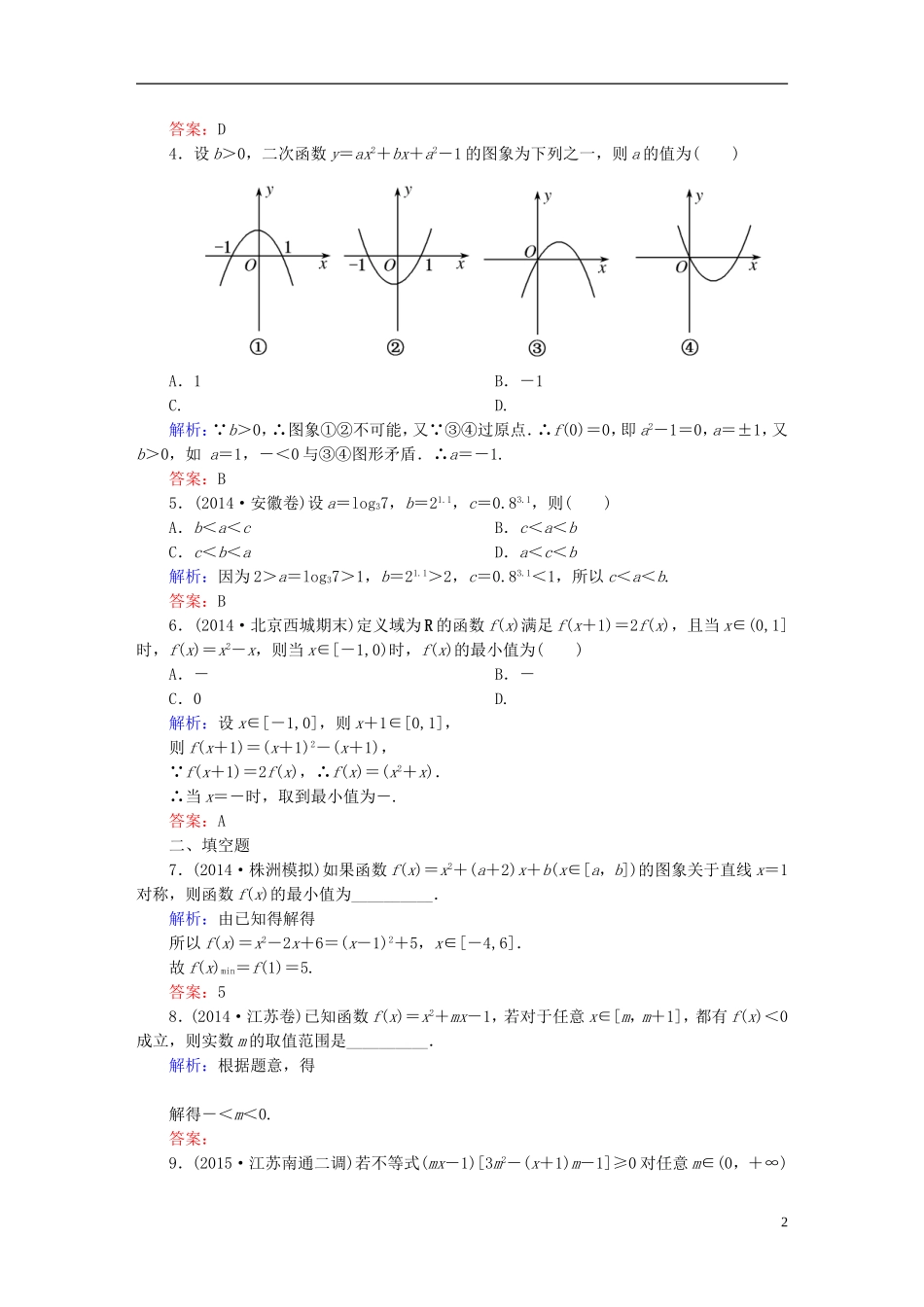
课时作业6二次函数与幂函数一、选择题1.(2015·九江七校联考)已知二次函数f(x)=ax2+bx+c,其中abc<0,则函数图象可能是()ABCD解析:当a<0时,开口向下,因为abc<0,所以b,c同号.对于A图象可知c>0,则b>0,所以->0,A错;由B图可知c<0,故b<0,所以-<0,即函数的对称轴在y轴左侧,B错;当a>0时,因为abc<0,所以b,c异号,由C,D图象可知c<0,故b>0,所以-<0,即函数的对称轴在y轴左侧,故选C.答案:C2.(2015·湖北孝感调研)函数f(x)=(m2-m-1)xm是幂函数,且在(0,+∞)上为增函数,则实数m的值是()A.-1B.2C.3D.-1或2解析:f(x)=(m2-m-1)xm是幂函数⇒m2-m-1=1⇒m=-1或m=2.又f(x)在(0,+∞)上是增函数,所以m=2.答案:B3.(2014·山东威海一模)若a>b,则下列不等式成立的是()A.lna>lnbB.0.3a>0.3bC.a>bD.>解析:取a=2,b=-1,可知lnb,b无意义,故A,C错;y=0.3x是减函数,又a>b,则0.3a<0.3b,故B错;y=x在(-∞,+∞)是增函数,又a>b,则a>b,即>成立,故选D.1答案:D4.设b>0,二次函数y=ax2+bx+a2-1的图象为下列之一,则a的值为()A.1B.-1C.D.解析: b>0,∴图象①②不可能,又 ③④过原点.∴f(0)=0,即a2-1=0,a=±1,又b>0,如a=1,-<0与③④图形矛盾.∴a=-1.答案:B5.(2014·安徽卷)设a=log37,b=21.1,c=0.83.1,则()A.b<a<cB.c<a<bC.c<b<aD.a<c<b解析:因为2>a=log37>1,b=21.1>2,c=0.83.1<1,所以c<a<b.答案:B6.(2014·北京西城期末)定义域为R的函数f(x)满足f(x+1)=2f(x),且当x∈(0,1]时,f(x)=x2-x,则当x∈[-1,0)时,f(x)的最小值为()A.-B.-C.0D.解析:设x∈[-1,0],则x+1∈[0,1],则f(x+1)=(x+1)2-(x+1), f(x+1)=2f(x),∴f(x)=(x2+x).∴当x=-时,取到最小值为-.答案:A二、填空题7.(2014·株洲模拟)如果函数f(x)=x2+(a+2)x+b(x∈[a,b])的图象关于直线x=1对称,则函数f(x)的最小值为__________.解析:由已知得解得所以f(x)=x2-2x+6=(x-1)2+5,x∈[-4,6].故f(x)min=f(1)=5.答案:58.(2014·江苏卷)已知函数f(x)=x2+mx-1,若对于任意x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是__________.解析:根据题意,得解得-<m<0.答案:9.(2015·江苏南通二调)若不等式(mx-1)[3m2-(x+1)m-1]≥0对任意m∈(0,+∞)2恒成立,则实数x的值为__________.解析:根据题意可令f(m)=xm-1,易得图象恒过点(0,-1),令f(m)=0,可得m=.又令g(m)=3m2-(x+1)m-1,易得图象恒过点(0,-1),要使不等式(mx-1)[3m2-(x+1)m-1]≥0对任意m∈(0,+∞)恒成立,则要满足代入可得x=1.答案:1三、解答题10.已知函数f(x)=x2+2x·tanθ-1,x∈,其中θ∈.(1)当θ=-时,求函数f(x)的最大值与最小值;(2)求θ的取值范围,使y=f(x)在区间上是单调函数.解析:(1)当θ=-时,f(x)=x2-x-1=2-,x∈,∴x=时,f(x)的最小值为-.x=-1时,f(x)的最大值为.(2)函数f(x)=(x+tanθ)2-1-tan2θ, y=f(x)在区间上是单调函数,∴-tanθ≤-1或-tanθ≥,即tanθ≥1或tanθ≤-.因此,θ的取值范围是∪.11.(2015·汕头四中月考)已知函数f(x)是二次函数,不等式f(x)<0的解集是(0,5),且f(x)在区间[-1,4]上的最大值为12.(1)求f(x)的解析式;(2)设函数f(x)在[t,t+1]上的最小值为g(t),求g(t)的表达式.解析:(1)因为f(x)是二次函数,且f(x)<0的解集是(0,5),所以可设f(x)=ax(x-5)(a>0).所以f(x)在区间[-1,4]上的最大值是f(-1)=6a.由已知,得6a=12,所以a=2.所以f(x)=2x(x-5)=2x2-10x(x∈R).(2)由(1)知f(x)=2x2-10x=22-,开口向上,对称轴为x=,①当t+1≤,即t≤时,f(x)在[t,t+1]上单调递减,所以g(t)=2(t+1)2-10(t+1)=2t2-6t-8;②当t≥时,f(x)在[t,t+1]上单调递增,所以g(t)=2t2-10t;③当t<<t+1,即<t<时,f(x)在对称轴处取得最小值,所以g(t)=f=-.综上所述,g(t)=12.(2015·银川质检)已知f(x)是二次函数,不等式f(x)<0的解集是(0,5),且f...