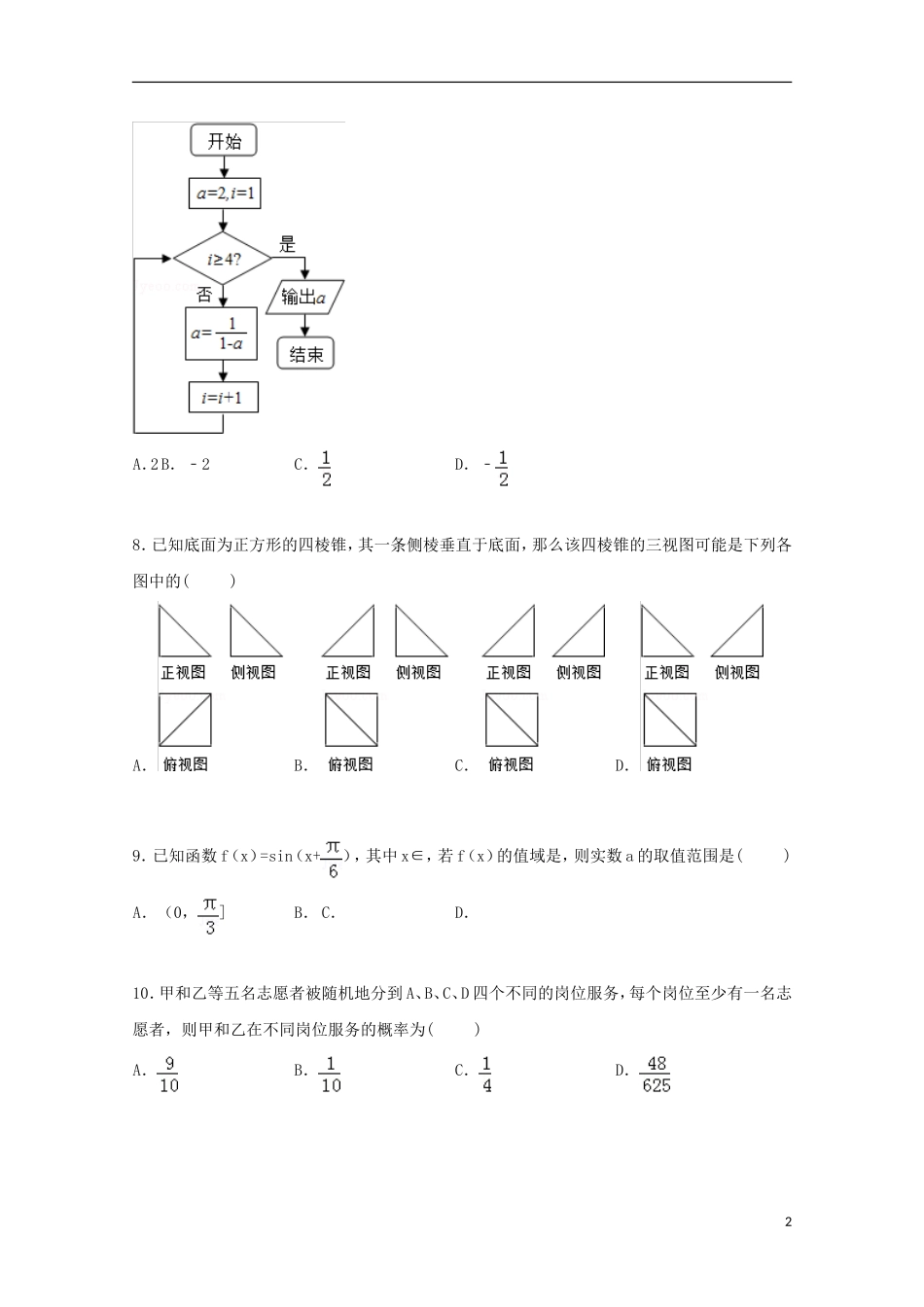
广西南宁市2015届高考数学一模试卷(理科)一.选择题1.已知全集U=R,A={x|x2+3x﹣10>0},B={x|﹣2≤x≤5},则(∁UA)∩B等于()A.{x|﹣5<x≤2}B.{x|﹣2<x≤5}C.{x|﹣2≤x≤2}D.{x|﹣5≤x≤5}2.设复数z满足z•(1﹣i)=2,则复数z的模|z|等于()A.B.2C.D.43.设等比数列{an}的前n项和为Sn,若a1=1,a4=﹣8,则S5等于()A.﹣11B.11C.331D.﹣314.下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数是()A.y=lnxB.y=x2C.y=cosxD.y=2﹣|x|5.(1﹣)5的展开式x2的系数是()A.﹣5B.5C.﹣10D.106.已知x,y满足则目标函数z=x+y的最大值为()A.4B.5C.6D.77.如图所示的程序框图中输出的a的结果为()1A.2B.﹣2C.D.﹣8.已知底面为正方形的四棱锥,其一条侧棱垂直于底面,那么该四棱锥的三视图可能是下列各图中的()A.B.C.D.9.已知函数f(x)=sin(x+),其中x∈,若f(x)的值域是,则实数a的取值范围是()A.(0,]B.C.D.10.甲和乙等五名志愿者被随机地分到A、B、C、D四个不同的岗位服务,每个岗位至少有一名志愿者,则甲和乙在不同岗位服务的概率为()A.B.C.D.211.双曲线与抛物线y2=2px(p>0)相交于A,B两点,公共弦AB恰好过它们的公共焦点F,则双曲线C的离心率为()A.B.C.D.12.定义域为的函数y=f(x)的图象的两个端点A、B,M(x,y)是f(x)图象上任意一点,其中x=λa+(1﹣λ)b(λ∈R),向量=λ+(1﹣λ),其中O为坐标原点,若不等式||≤k恒成立,则称函数f(x)在上“k阶线性近似”.若函数y=x+在上“k阶线性近似”,则实数k的取值范围为()A.(2)若acosB+bcosA=2,a=,求sinA的值.18.某网站用“10分制”调查一社区人们的治安满意度,现从调查人群中随机抽取16名,以下茎叶图记录了他们的治安满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):(1)若治安满意度不低于9.5分,则称该人的治安满意度为“极安全”.求从这16人中随机选取3人,至多有1人是“极安全”的概率;(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记X表示抽到“极安全”的人数,求X的分布列及数学期望.19.如图,在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AB=BC=CA=AA1,D为AB的中点.(1)求证:BC1∥平面DCA1;(2)求二面角D﹣CA1﹣C1的平面角的余弦值.320.已知椭圆+=1(a>b>0)的离心率为,且过点(,).(1)求椭圆C的方程;(2)设椭圆的左、右顶点分别为A、B,点S是椭圆上位于x轴上方的动点,直线AS,BS与直线l:x=分别交于M、N两点,求线段MN长度的最小值.21.已知函数f(x)=xlnx+ax(a∈R)(I)若函数f(x)在区间则其三视图如图:,故选:C.点评:本题考查简单几何体的三视图,考查空间想象能力,是基础题.9.已知函数f(x)=sin(x+),其中x∈,若f(x)的值域是,则实数a的取值范围是()A.(0,]B.C.D.考点:正弦函数的图象.专题:三角函数的图像与性质.4分析:先求得x+的取值范围,由x+∈时f(x)的值域是,可知≤a+≤,可解得实数a的取值范围.解答:解: x∈,∴x+∈, x+∈时f(x)的值域是,∴由函数的图象和性质可知≤a+≤,可解得a∈.故选:D.点评:本题主要考察了正弦函数的图象和性质,由函数的图象和性质得到不等式≤a+≤是解题的关键,属于基本知识的考查.10.甲和乙等五名志愿者被随机地分到A、B、C、D四个不同的岗位服务,每个岗位至少有一名志愿者,则甲和乙在不同岗位服务的概率为()A.B.C.D.考点:古典概型及其概率计算公式.专题:概率与统计.分析:所有的结果共有C52A44种,不满足条件的事件数A44,可得不满足条件的概率,用1减去此概率即得所求.解答:解:5个人分到4个岗位,每个岗位至少有一名志愿者共有C52A44=240种结果,甲和乙在同一岗位服务的事件数A44=24则甲和乙不在同一岗位服务的概率为1﹣=故选:A点评:本题主要考查古典概型和排列组合,排列与组合问题要区分开,若题目要求元素的顺序则是排列问题,排列问题要做到不重不漏,有些题目带有一定的约束条件,解题时要先考虑有限制条件的元素,属于中档题.511.双曲线与...